Contents
内挿関数とガウス積分
要素内任意点の物理量を節点物理量で表現する
四角形要素を用いた有限要素法では,要素内任意点の物理量を,内挿関数 $[\boldsymbol{N}]$ を用いて,要素を構成する節点の物理量で表す必要がある.ここでは,要素での積分にはガウス積分を用いることとし,$[−1,1]$ の範囲を有する正規化パラメータ座標 $(a,b)$ を用いて,物理量を表現することを考える.
以下に,各種2次元問題における,要素内任意位置での物理量を,節点での物理量で表した事例を示す.
2次元弾性問題
四角形要素内任意点の変位 $u$,$v$ を,節点変位 $(u_i,v_i)$,$(u_j,v_j)$,$(u_k,v_k)$,$(u_l,v_l)$ を用い以下のように仮定する.
\begin{align}
u=&N_1(a,b)\cdot u_i+N_2(a,b)\cdot u_j+N_3(a,b)\cdot u_k+N_4(a,b)\cdot u_l \\
v=&N_1(a,b)\cdot v_i+N_2(a,b)\cdot v_j+N_3(a,b)\cdot v_k+N_4(a,b)\cdot v_l
\end{align}
要素内任意点の変位を $\{\boldsymbol{u}\}$,節点変位を $\{\boldsymbol{u_{nd}}\}$ とすれば,
\begin{equation}
\{\boldsymbol{u}\}=\begin{Bmatrix} u \\ v \end{Bmatrix}
=\begin{bmatrix}
N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4 & 0 \\
0 & N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4
\end{bmatrix}
\begin{Bmatrix}
u_i \\ v_i \\ u_j \\ v_j \\ u_k \\ v_k \\ u_l \\ v_l
\end{Bmatrix}
=[\boldsymbol{N}]\{\boldsymbol{u_{nd}}\}
\end{equation}
2次元浸透流問題
四角形要素内任意点の全水頭 $\phi$ を,節点水頭 $h_i$,$h_j$,$h_k$,$h_l$ を用い以下のように仮定する.
\begin{equation}
\phi=N_1(a,b)\cdot h_i+N_2(a,b)\cdot h_j+N_3(a,b)\cdot h_k+N_4(a,b)\cdot h_l
\end{equation}
要素内任意点の水頭を $\phi$,節点水頭を $\{\boldsymbol{h}\}$ とすれば,
\begin{equation}
\phi=\begin{bmatrix} N_1 & N_2 & N_3 & N_4 \end{bmatrix}\{\boldsymbol{h}\}=[\boldsymbol{N}]\{\boldsymbol{h}\}
\end{equation}
2次元熱伝導問題
四角形要素内任意点の温度$T$を節点温度 $\phi_i$,$\phi_j$,$\phi_k$,$\phi_l$ を用い以下のように仮定する.
\begin{equation}
T=N_1(a,b)\cdot \phi_i+N_2(a,b)\cdot \phi_j+N_3(a,b)\cdot \phi_k+N_4(a,b)\cdot \phi_l
\end{equation}
要素内任意点の温度を $T$,節点温度を $\{\boldsymbol{\phi}\}$ とすれば,
\begin{equation}
T=\begin{bmatrix}N_1 & N_2 & N_3 & N_4 \end{bmatrix}\{\boldsymbol{\phi}\}=[\boldsymbol{N}]\{\boldsymbol{\phi}\}
\end{equation}
内挿関数とその微分
実際の計算においては,内挿関数の数式表現とその微分が必要となるため,これらを求めておくことにする.
以下,$(a,b)$ は,$a=[−1,1]$,$b=[−1,1]$ の範囲を有する正規化パラメータ座標である.
内挿関数の数式表現
\begin{align}
N_1=&\frac{1}{4}(1-a)(1-b) \qquad N_2=\frac{1}{4}(1+a)(1-b) \\
N_3=&\frac{1}{4}(1+a)(1+b) \qquad N_4=\frac{1}{4}(1-a)(1+b)
\end{align}
内挿関数の微分
\begin{align}
&\cfrac{\partial N_1}{\partial a}=-\cfrac{1}{4}(1-b) &\cfrac{\partial N_2}{\partial a}=+\cfrac{1}{4}(1-b) & &\cfrac{\partial N_3}{\partial a}=+\cfrac{1}{4}(1+b) & &\cfrac{\partial N_4}{\partial a}=-\cfrac{1}{4}(1+b) \\
&\cfrac{\partial N_1}{\partial b}=-\cfrac{1}{4}(1-a) &\cfrac{\partial N_2}{\partial b}=-\cfrac{1}{4}(1+a) & &\cfrac{\partial N_3}{\partial b}=+\cfrac{1}{4}(1+a) & &\cfrac{\partial N_4}{\partial b}=+\cfrac{1}{4}(1-a)
\end{align}
ここで,内挿関数 $N_i$ に関する微分は,Jacobi行列 $[J]$ を用いて以下の通り表せる.
\begin{equation}
\begin{Bmatrix} \cfrac{\partial N_i}{\partial a} \\ \cfrac{\partial N_i}{\partial b} \end{Bmatrix}
=[J] \begin{Bmatrix} \cfrac{\partial N_i}{\partial x} \\ \cfrac{\partial N_i}{\partial y} \end{Bmatrix} \qquad
\begin{Bmatrix} \cfrac{\partial N_i}{\partial x} \\ \cfrac{\partial N_i}{\partial y} \end{Bmatrix}
=[J]^{-1} \begin{Bmatrix} \cfrac{\partial N_i}{\partial a} \\ \cfrac{\partial N_i}{\partial b} \end{Bmatrix}
\end{equation}
\begin{equation}
[J]=\begin{bmatrix}
\cfrac{\partial x}{\partial a} & \cfrac{\partial y}{\partial a} \\
\cfrac{\partial x}{\partial b} & \cfrac{\partial y}{\partial b}
\end{bmatrix}
=\begin{bmatrix}
\displaystyle \sum_{i=1}^4\left(\cfrac{\partial N_i}{\partial a}x_i\right) & \displaystyle \sum_{i=1}^4\left(\cfrac{\partial N_i}{\partial a}y_i\right) \\
\displaystyle \sum_{i=1}^4\left(\cfrac{\partial N_i}{\partial b}x_i\right) & \displaystyle \sum_{i=1}^4\left(\cfrac{\partial N_i}{\partial b}y_i\right)
\end{bmatrix}
=\begin{bmatrix} J_{11} & J_{12} \\ J_{21} & J_{22} \end{bmatrix}
\end{equation}
\begin{equation}
[J]^{-1}=\frac{1}{\det(J)}\begin{bmatrix} J_{22} & -J_{12} \\ -J_{21} & J_{11} \end{bmatrix} \qquad
\det(J)=J_{11}\cdot J_{22}-J_{12}\cdot J_{21}
\end{equation}
上記より,
\begin{equation}
\cfrac{\partial N_i}{\partial x}=\cfrac{1}{\det(J)}\left\{J_{22}\cfrac{\partial N_i}{\partial a}-J_{12}\cfrac{\partial N_i}{\partial b}\right\} \qquad
\cfrac{\partial N_i}{\partial y}=\cfrac{1}{\det(J)}\left\{-J_{21}\cfrac{\partial N_i}{\partial a}+J_{11}\cfrac{\partial N_i}{\partial b}\right\}
\end{equation}
以下に$[J]$の要素を示す.ここに$x_{i,j,k,l}$および$y_{i,j,k,l}$は要素を構成する節点座標である.
\begin{align}
&J_{11}=\frac{\partial N_1}{\partial a} x_i+\frac{\partial N_2}{\partial a} x_j+\frac{\partial N_3}{\partial a} x_k+\frac{\partial N_4}{\partial a} x_l \\
&J_{12}=\frac{\partial N_1}{\partial a} y_i+\frac{\partial N_2}{\partial a} y_j+\frac{\partial N_3}{\partial a} y_k+\frac{\partial N_4}{\partial a} y_l \\
&J_{21}=\frac{\partial N_1}{\partial b} x_i+\frac{\partial N_2}{\partial b} x_j+\frac{\partial N_3}{\partial b} x_k+\frac{\partial N_4}{\partial b} x_l \\
&J_{22}=\frac{\partial N_1}{\partial b} y_i+\frac{\partial N_2}{\partial b} y_j+\frac{\partial N_3}{\partial b} y_k+\frac{\partial N_4}{\partial b} y_l
\end{align}
以上により,$[J]$ の各要素が定まり,$[\boldsymbol{N}]$ の微分値も定めることができる.
なお,この段階では $[J]$ および $[\boldsymbol{N}]$ とその微分値は,変数 $a$ および $b$ の関数として定義されていることに注意が必要である.
ガウス積分
積分は以下に示すガウス積分により行う.
面積積分
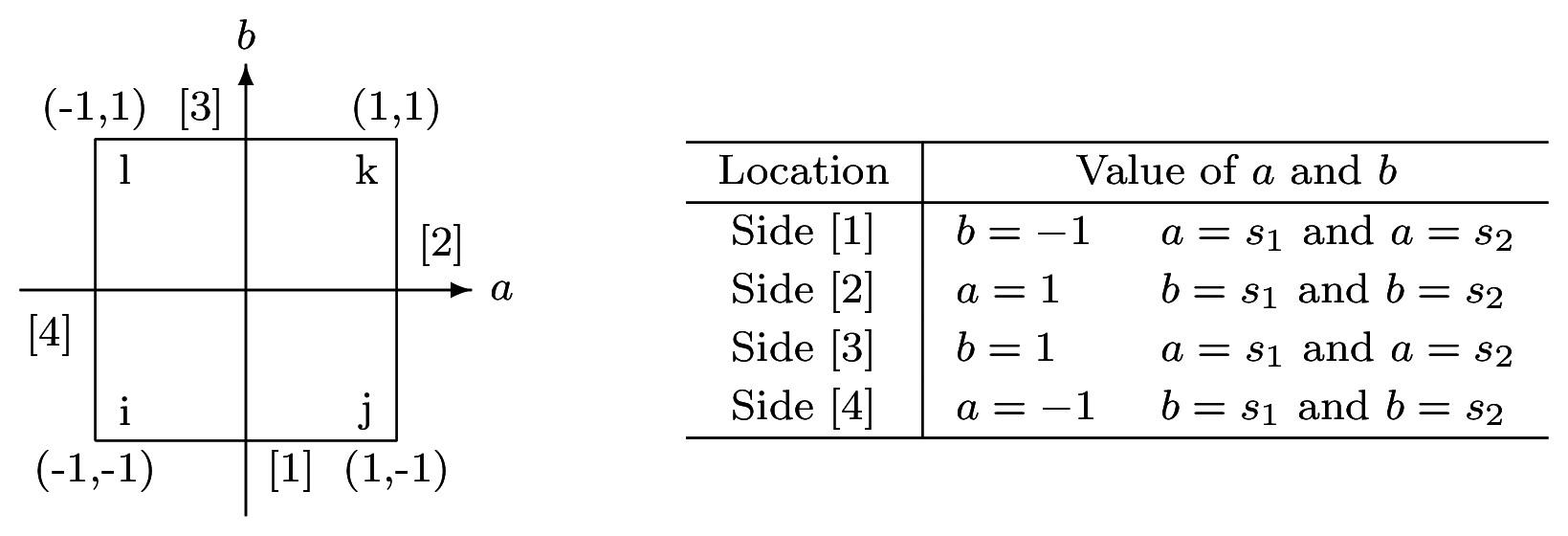
積分点を 4 点 ($n=2$) とすれば,$a$,$b$ および重み $H$ の値は下表の通りであり,$a$,$b$ を変化させた 4 回の値の総和が積分の近似値となる.また,重みが $H=1$ であることから,計算は更に単純になる.
\begin{equation}
\int_{-1}^{1}\int_{-1}^{1} f(a,b)\cdot da\cdot db
\doteqdot \sum_{i=1}^n\sum_{j=1}^n H_i\cdot H_j\cdot f(a_i,b_j)
= \sum_{kk=1}^4 f(a_{kk}, b_{kk})
\end{equation}
| i | j | a | b | H | kk |
|---|
| 1 | 1 | -0.57735 02692 | -0.57735 02692 | 1.00000 00000 | 1 |
| 1 | 2 | +0.57735 02692 | -0.57735 02692 | 1.00000 00000 | 2 |
| 2 | 1 | +0.57735 02692 | +0.57735 02692 | 1.00000 00000 | 3 |
| 2 | 2 | -0.57735 02692 | +0.57735 02692 | 1.00000 00000 | 4 |
線積分
熱伝導解析では,熱伝達境界は要素の辺で指定されるため,線積分を行う必要がある.その考え方を以下に示す.
正規化された座標系 a-b において,節点 i-j 間を辺 [1],節点 j-k 間を辺 [2],節点 k-l 間を辺 [3],節点 l-i 間を 辺 [4] とする.例えば,辺 [1] において境界条件が指定された場合,内挿関数 [N ] において b = −1 とし,面積積分の場合の表 の a = s1 および a = s2 の [N] 値の総和を求めればよいことになる.
線積分の場合の積分点座標 s および重みは下表の通りである.
| s1 | s2 | H |
|---|
| -0.57735 02692 | +0.57735 02692 | 1.00000 00000 |
仮想仕事の式による要素剛性方程式の標準的な形式の導出
仮想仕事の式による要素剛性方程式の標準的な形式の導出を行う.
一般に,外力を受ける物体が静的釣り合い状態にある場合,物体内部の応力による仮想仕事と表面力などの外力による仮想仕事は等しい関係にある.この関係を式で表すと以下の通りとなる.
\begin{equation}
\int_V \{\boldsymbol{\delta \epsilon}\}\{\boldsymbol{\sigma}\}dV=\int_A \{\boldsymbol{\delta u}\}\{\boldsymbol{S}\}dA+\int_V \{\boldsymbol{\delta u}\}\{\boldsymbol{F}\}dV
\end{equation}
| $\{\boldsymbol{\delta \epsilon}\}$ | :応力方向の仮想ひずみ | $\{\boldsymbol{\sigma}\}$ | :物体内部応力 |
| $\{\boldsymbol{\delta u}\}$ | :表面力方向の仮想変位 | $\{\boldsymbol{S}\}$ | :表面力 |
| $V$ | :物体の体積 | $\{\boldsymbol{F}\}$ | :物体力(慣性力) |
| $A$ | :表面力が作用する領域面積 | | |
ここで,物体を1つの有限要素とし,要素内任意点のひずみ$\{\boldsymbol{\epsilon}\}$および要素内任意点の変位$\{\boldsymbol{u}\}$を,以下のように節点変位$\{\boldsymbol{u_{nd}}\}$で表せたとする.
\begin{align}
&\{\boldsymbol{\epsilon}\}=[\boldsymbol{B}]\{\boldsymbol{u_{nd}}\} \\
&\{\boldsymbol{u}\}=[\boldsymbol{N}]\{\boldsymbol{u_{nd}}\}
\end{align}
ここに,$[\boldsymbol{B}]$はひずみ-変位関係行列,$[\boldsymbol{N}]$は内挿関数行列である.
また以下に示す線形弾性体の応力-ひずみ関係を導入する.
\begin{equation}
\{\boldsymbol{\sigma}\}=[\boldsymbol{D_e}]\{\boldsymbol{\epsilon}-\boldsymbol{\epsilon_0}\}
\end{equation}
$[\boldsymbol{D_e}]$は応力-ひずみ関係行列,$\{\boldsymbol{\epsilon_0}\}$は温度変化などによる初期歪である.
次に物体力$\{\boldsymbol{F}\}$は,内挿関数と節点での慣性力$\{\boldsymbol{w_{nd}}\}$を用いて以下のように表せるものとする.
\begin{equation}
\{\boldsymbol{F}\}=[\boldsymbol{N}]\{\boldsymbol{w_{nd}}\}
\end{equation}
上記関係を用いることにより,仮想仕事式の左辺(内力による仮想仕事)は以下のようになる.
\begin{align}
\int_V \{\boldsymbol{\delta \epsilon}\}\{\boldsymbol{\sigma}\}dV
=&\{\boldsymbol{\delta u_{nd}}\}^T \int_v[\boldsymbol{B}]^T\{\boldsymbol{\sigma}\}dV \\
=&\{\boldsymbol{\delta u_{nd}}\}^T \left(\int_V[\boldsymbol{B}]^T[\boldsymbol{D_e}][\boldsymbol{B}]dV\right) \{\boldsymbol{u_{nd}}\}
-\{\boldsymbol{\delta u_{nd}}\}^T \left(\int_V[\boldsymbol{B}]^T[\boldsymbol{D_e}]\{\boldsymbol{\epsilon_0}\}dV\right) \\
=&\{\boldsymbol{\delta u_{nd}}\}^T[\boldsymbol{k}]\{\boldsymbol{u_{nd}}\}-\{\boldsymbol{\delta u_{nd}}\}^T\{\boldsymbol{f_t}\}
\end{align}
また,仮想仕事式の右辺(外力による仮想仕事)は以下のようになる.
\begin{align}
&\int_A \{\boldsymbol{\delta u}\}\{\boldsymbol{S}\}dA=\{\boldsymbol{\delta u_{nd}}\}^T \left(\int_A [\boldsymbol{N}]^T\{\boldsymbol{S}\}dA\right)=\{\boldsymbol{\delta u_{nd}}\}^T\{\boldsymbol{f}\} \\
&\int_V \{\boldsymbol{\delta u}\}\{\boldsymbol{F}\}dV=\{\boldsymbol{\delta u_{nd}}\}^T \left(\int_V [\boldsymbol{N}]^T [\boldsymbol{N}]dV\right)\{\boldsymbol{w_{nd}}\}=\{\boldsymbol{\delta u_{nd}}\}^T\{\boldsymbol{f_b}\}
\end{align}
以上により,次に示すような,一般的な剛性方程式の形が得られる.
\begin{equation}
[\boldsymbol{k}]\{\boldsymbol{u_{nd}}\}=\{\boldsymbol{f}\}+\{\boldsymbol{f_t}\}+\{\boldsymbol{f_b}\}
\end{equation}
\begin{align}
&[\boldsymbol{k}]=\int_V[\boldsymbol{B}]^T[\boldsymbol{D_e}][\boldsymbol{B}]dV & & \text{(要素剛性行列)}\\
&\{\boldsymbol{f}\}=\int_A [\boldsymbol{N}]^T\{\boldsymbol{S}\}dA & & \text{(節点外力ベクトル)}\\
&\{\boldsymbol{f_t}\}=\int_V[\boldsymbol{B}]^T[\boldsymbol{D_e}]\{\boldsymbol{\epsilon_0}\}dV & & \text{(節点初期歪ベクトル)}\\
&\{\boldsymbol{f_b}\}=\left(\int_V [\boldsymbol{N}]^T [\boldsymbol{N}]dV\right)\{\boldsymbol{w_{nd}}\} & & \text{(節点慣性力ベクトル)}
\end{align}
上式は,変位を求めるための式であり,初期歪は荷重項として扱っている.要素内部応力は,前出式
\begin{equation}
\{\boldsymbol{\sigma}\}=[\boldsymbol{D_e}]\{\boldsymbol{\epsilon}-\boldsymbol{\epsilon_0}\}
\end{equation}
を用いて計算する必要があることに注意する.ここに,$\{\boldsymbol{\epsilon}\}$ は,剛性方程式を解いて求めた変位から求めた要素の歪ベクトルである.
2次元弾性骨組構造解析
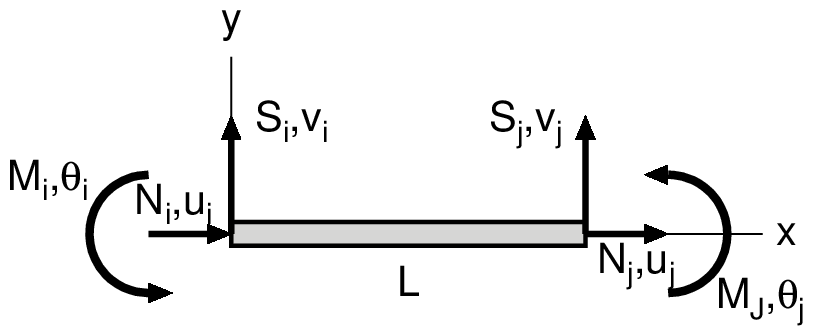
要素剛性方程式
要素剛性方程式は,以下に示すとおりである.
\begin{equation}
\{\boldsymbol{f}\}=[\boldsymbol{k}]\{\boldsymbol{u}\}
\end{equation}
\begin{equation}
\begin{Bmatrix} N_i \\ S_i \\ M_i \\ N_j \\ S_j \\ M_j \end{Bmatrix}
=\begin{bmatrix}
EA/L & 0 & 0 & -EA/L & 0 & 0 \\
0 & 12 EI/L^3 & 6 EI/L^2 & 0 & -12 EI/L^3 & 6 EI/L^2 \\
0 & 6 EI/L^2 & 4 EI/L & 0 & -6 EI/L^2 & 2 EI/L \\
-EA/L & 0 & 0 & EA/L & 0 & 0 \\
0 & -12 EI/L^3 & -6 EI/L^2 & 0 & 12 EI/L^3 & -6 EI/L^2 \\
0 & 6 EI/L^2 & 2 EI/L & 0 & -6 EI/L^2 & 4 EI/L
\end{bmatrix}
\begin{Bmatrix} u_i \\ v_i \\ \theta_i \\ u_j \\ v_j \\ \theta_j \end{Bmatrix}
\end{equation}
| $EA$ | 軸剛性 | | $N$ | 軸力 | | $u$ | 軸方向変位 (x方向変位) |
| $EI$ | 曲げ剛性 | | $S$ | せん断力 | | $v$ | たわみ (y方向変位) |
| $L$ | 要素長 | | $M$ | 曲げモーメント | | $\theta$ | 回転量 |
 |
 |
| 要素自由度 | 要素座標系(x-y)および全体座標系(X−Y) |
|---|
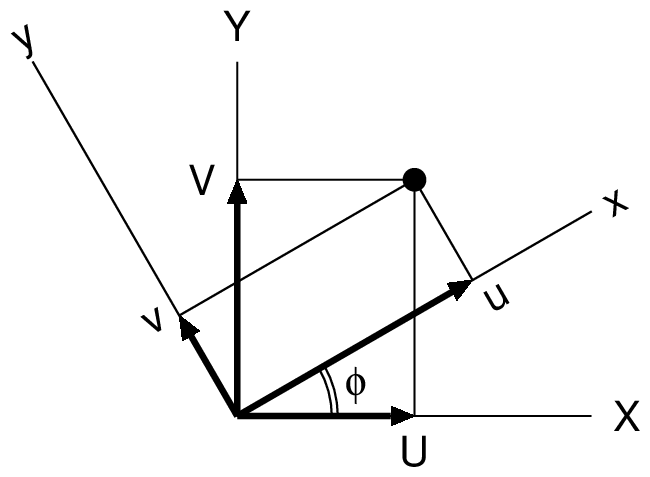
座標変換行列
全体座標系から要素座標系への座標変換マトリックスは以下に示すとおりである.
\begin{equation}
\{\boldsymbol{u}\}=[\boldsymbol{T}]\{\boldsymbol{U}\}
\end{equation}
\begin{equation}
\begin{Bmatrix} u_i \\ v_i \\ \theta_i \\ u_j \\ v_j \\ \theta_j \end{Bmatrix}
=
\begin{bmatrix}
\cos\phi & \sin\phi & 0 & 0 & 0 & 0 \\
-\sin\phi & \cos\phi & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & \cos\phi & \sin\phi & 0 \\
0 & 0 & 0 & -\sin\phi & \cos\phi & 0 \\
0 & 0 & 0 & 0 & 0 & 1
\end{bmatrix}
\begin{Bmatrix} U_i \\ V_i \\ \Theta_i \\ U_j \\ V_j \\ \Theta_j \end{Bmatrix}
\end{equation}
全体剛性方程式
系全体で組み立てた全体剛性方程式は,以下のようになる.
\begin{equation}
[\boldsymbol{K}]\{\boldsymbol{U}\}=\{\boldsymbol{F}\}+\{\boldsymbol{F_t}\}+\{\boldsymbol{F_b}\}
\end{equation}
| $[\boldsymbol{K}]=[\boldsymbol{T}]^T[\boldsymbol{k}][\boldsymbol{T}]$ | :全体剛性行列 |
| $\{\boldsymbol{U}\}$ | :全体座標系変位ベクトル |
| $\{\boldsymbol{F}\}$ | :全体座標系節点外力ベクトル |
| $\{\boldsymbol{F_t}\}=[\boldsymbol{T}]^T\{\boldsymbol{f_t}\}$ | :全体座標系節点温度荷重ベクトル |
| $\{\boldsymbol{F_b}\}=\{\boldsymbol{f_b}\}$ | :全体座標系節点慣性力ベクトル |
\begin{equation}
\{\boldsymbol{f_t}\}
=\begin{Bmatrix} -EA\cdot\alpha\cdot\Delta T \\ 0 \\ 0 \\ EA\cdot\alpha\cdot\Delta T \\ 0 \\ 0 \end{Bmatrix}
\qquad\qquad\qquad
\{\boldsymbol{f_b}\}
=\cfrac{\gamma A \ell}{2} \begin{Bmatrix} k_h \\ k_v \\ 0 \\ k_h \\ k_v \\ 0 \end{Bmatrix}
\end{equation}
| $EA$ | :軸剛性 | $\alpha$ | :線膨張係数 | $\Delta T$ | :温度変化量 |
| $\gamma$ | :単位体積重量 | $A$ | :要素断面積 | $\ell$ | :要素長さ |
| $k_h$ | :水平加速度 | $k_v$ | :鉛直加速度 | | |
ここで,要素節点温度荷重ベクトル $\{\boldsymbol{f_t}\}$ は部材の軸力の補正項なので,全体剛性方程式に組み込む場合,座標変換が必要であるが,節点慣性力ベクトル $\{\boldsymbol{f_b}\}$ は,加速度の方向が全体座標系で定義されているので,全体剛性方程式に組み込む場合,座標変換は不要であることに注意する.
また,全体剛性方程式の解としての変位から部材断面力を算出する場合,軸力については以下の温度変化の補正を行う必要が有ることに注意する.
\begin{align}
N_{i}'=N_i+EA\cdot\alpha\cdot\Delta T \\
N_{j}'=N_j-EA\cdot\alpha\cdot\Delta T
\end{align}
2次元弾性トラス構造解析
要素剛性方程式
2次元トラス構造解析の要素剛性は,2次元骨組構造解析用要素剛性から,モーメント・回転量に関する自由度を除いたものになる.座標変換行列も同様に,モーメント・回転量に関する項を除いたものになる.
2次元トラス構造解析用要素剛性方程式は,以下に示すとおりである.
\begin{equation*}
\begin{Bmatrix} N_i \\ S_i \\ N_j \\ S_j \end{Bmatrix}
=\begin{bmatrix}
EA/L & 0 & -EA/L & 0 \\
0 & 0 & 0 & 0 \\
-EA/L & 0 & EA/L & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}
\begin{Bmatrix} u_i \\ v_i \\ u_j \\ v_j \end{Bmatrix}
\end{equation*}
| $EA$ | 軸剛性 | | $N$ | 軸力 | | $u$ | x方向変位 |
| $L$ | 要素長 | | $S$ | せん断力 | | $v$ | y方向変位 |
座標変換行列は,以下に示すとおりである.
\begin{equation}
\begin{Bmatrix} u_i \\ v_i \\ u_j \\ v_j \end{Bmatrix}
=
\begin{bmatrix}
\cos\phi & \sin\phi & 0 & 0 \\
-\sin\phi & \cos\phi & 0 & 0 \\
0 & 0 & \cos\phi & \sin\phi \\
0 & 0 & -\sin\phi & \cos\phi \\
\end{bmatrix}
\begin{Bmatrix} U_i \\ V_i \\ U_j \\ V_j \end{Bmatrix}
\end{equation}
格子桁構造解析
要素剛性方程式
格子桁構造解析の要素剛性と2次元骨組構造解析用要素剛性の関係は,以下の通りで,剛性行列を書き換えることにより,相互に利用可能となる.
| 格子桁 | 2次元骨組 |
|---|
| ねじりモーメント | 軸力 |
| 曲げモーメント | せん断力 |
| せん断力 | 曲げモーメント |
格子桁構造解析用の要素剛性方程式は,以下に示すとおりである.
\begin{equation*}
\begin{Bmatrix} T_i \\ M_i \\ Q_i \\ T_j \\ M_j \\ Q_j \end{Bmatrix}
=\begin{bmatrix}
GJ/L & 0 & 0 & -GJ/L & 0 & 0 \\
0 & 4 EI/L & -6 EI/L^2 & 0 & 2 EI/L & 6 EI/L^2 \\
0 & -6 EI/L^2 & 12 EI/L^3 & 0 & -6 EI/L^2 & -12 EI/L^3 \\
-GJ/L & 0 & 0 & GJ/L & 0 & 0 \\
0 & 2 EI/L & -6 EI/L^2 & 0 & 4 EI/L & 6 EI/L^2 \\
0 & 6 EI/L^2 & -12 EI/L^3 & 0 & 6 EI/L^2 & 12 EI/L^3
\end{bmatrix}
\begin{Bmatrix} \phi_i \\ \theta_i \\ w_i \\ \phi_j \\ \theta_j \\ w_j \end{Bmatrix}
\end{equation*}
| $GJ$ | ねじり剛性 | | $T$ | ねじりモーメント | | $\phi$ | x軸回り回転量 |
| $EI$ | 曲げ剛性 | | $M$ | 曲げモーメント | | $\theta$ | y軸回り回転量 |
| $L$ | 要素長 | | $Q$ | せん断力 | | $w$ | z方向たわみ |
座標変換はX-Y平面内で行われるため,座標変換行列は,2次元骨組構造解析のものと同一となる.
 |
 |
| 全体座標系 | 要素座標系と要素自由度 |
|---|
(参考)充実矩形断面のねじり定数 $J$
コンクリートなどの充実矩形断面のねじり定数 $J$ は以下により計算できる.
\begin{equation}
J=\cfrac{h b^3}{3} \left\{1-\cfrac{192}{\pi^5} \cfrac{b}{h} \sum_{n=1}^\infty\left[\cfrac{1}{(2n-1)^5}\tanh\cfrac{(2n-1)\pi h}{2 b}\right]\right\} \qquad h \geqq b
\end{equation}
ここで,次式に示す係数 $\eta$ を導入すれば,係数 $\eta$ と部材寸法 $h/b$ の関係は以下の通りとなる.
\begin{equation}
J=\cfrac{h b^3}{\eta}
\end{equation}
| $h/b$ | 1 | 2 | 3 | 5 | 10 | 20 |
|---|
| $\eta$ | 7.114 | 4.373 | 3.798 | 3.433 | 3.202 | 3.098 |
|---|
上記計算は,以下に示す Python プログラムで行った.
import numpy as np
### Result ###
# h/b 1.0 2.0 3.0 5.0 10.0 20.0
# eta 7.114 4.373 3.798 3.433 3.202 3.098
# J=h*b**3/eta
n=100
b=1.0
#hh=np.arange(1.0,21.0,1.0)
hh=np.array([1.0,2.0,3.0,5.0,10.0,20.0])
for idx,elem in enumerate(hh):
h=elem
s=0.0
for i in range(1,n+1):
s=s+1/(2*i-1)**5*np.tanh((2*i-1)*np.pi*h/2/b)
x=1/3*(1-192/np.pi**5*b/h*s)
print('{0:10.3f} {1:10.3f}'.format(h/b,1/x))
3次元弾性骨組構造解析
要素剛性方程式
\begin{equation*}
\boldsymbol{\{f\}}=\boldsymbol{[k]}\boldsymbol{\{u\}}
\end{equation*}
節点変位ベクトル
\begin{equation*}
\boldsymbol{\{u\}}=
\begin{Bmatrix}
u_i & v_i & w_i & \theta_{xi} & \theta_{yi} & \theta_{zi} & u_j & v_j & w_j & \theta_{xj} & \theta_{yj} & \theta_{zj}
\end{Bmatrix}^T
\end{equation*}
\begin{align*}
& u & \text{: displacement in x-direction} & & & \theta_x & \text{: rotation around x-axis} \\
& v & \text{: displacement in y-direction} & & & \theta_y & \text{: rotation around y-axis} \\
& w & \text{: displacement in z-direction} & & & \theta_z & \text{: rotation around z-axis}
\end{align*}
節点力ベクトル
\begin{equation*}
\boldsymbol{\{f\}}=
\begin{Bmatrix}
N_i & S_{yi} & S_{zi} & M_{xi} & M_{yi} & M_{zi} & N_j & S_{yj} & S_{zj} & M_{xj} & M_{yj} & M_{zj}
\end{Bmatrix}^T
\end{equation*}
\begin{align*}
& N & \text{: axial force in x-direction} & & & M_x & \text{: moment around x-axis (tortional moment)} \\
& S_y & \text{: shear force in y-direction} & & & M_y & \text{: moment around y-axis (bending moment)} \\
& S_z & \text{: shear force in z-direction} & & & M_z & \text{: moment around z-axis (bending moment)}
\end{align*}
剛性行列
\begin{equation*}
\boldsymbol{[k]}=
\begin{bmatrix}
\cfrac{EA}{L} & 0 & 0 & 0 & 0 & 0 & -\cfrac{EA}{L} & 0 & 0 & 0 & 0 & 0 \\
0 & \cfrac{12EI_z}{L^3} & 0 & 0 & 0 & \cfrac{6EI_z}{L^2} & 0 & -\cfrac{12EI_z}{L^3} & 0 & 0 & 0 & \cfrac{6EI_z}{L^2} \\
0 & 0 & \cfrac{12EI_y}{L^3} & 0 & -\cfrac{6EI_y}{L^2} & 0 & 0 & 0 & -\cfrac{12EI_y}{L^3} & 0 & -\cfrac{6EI_y}{L^2} & 0 \\
0 & 0 & 0 & \cfrac{GJ}{L} & 0 & 0 & 0 & 0 & 0 & -\cfrac{GJ}{L} & 0 & 0 \\
0 & 0 & -\cfrac{6EI_y}{L^2} & 0 & \cfrac{4EI_y}{L} & 0 & 0 & 0 & \cfrac{6EI_y}{L^2} & 0 & \cfrac{2EI_y}{L} & 0 \\
0 & \cfrac{6EI_z}{L^2} & 0 & 0 & 0 & \cfrac{4EI_z}{L} & 0 & -\cfrac{6EI_z}{L^2} & 0 & 0 & 0 & \cfrac{2EI_z}{L} \\
-\cfrac{EA}{L} & 0 & 0 & 0 & 0 & 0 & \cfrac{EA}{L} & 0 & 0 & 0 & 0 & 0 \\
0 & -\cfrac{12EI_z}{L^3} & 0 & 0 & 0 & -\cfrac{6EI_z}{L^2} & 0 & \cfrac{12EI_z}{L^3} & 0 & 0 & 0 & -\cfrac{6EI_z}{L^2} \\
0 & 0 & -\cfrac{12EI_y}{L^3} & 0 & \cfrac{6EI_y}{L^2} & 0 & 0 & 0 & \cfrac{12EI_y}{L^3} & 0 & \cfrac{6EI_y}{L^2} & 0 \\
0 & 0 & 0 & -\cfrac{GJ}{L} & 0 & 0 & 0 & 0 & 0 & \cfrac{GJ}{L} & 0 & 0 \\
0 & 0 & -\cfrac{6EI_y}{L^2} & 0 & \cfrac{2EI_y}{L} & 0 & 0 & 0 & \cfrac{6EI_y}{L^2} & 0 & \cfrac{4EI_y}{L} & 0 \\
0 & \cfrac{6EI_z}{L^2} & 0 & 0 & 0 & \cfrac{2EI_z}{L} & 0 & -\cfrac{6EI_z}{L^2} & 0 & 0 & 0 & \cfrac{4EI_z}{L} \\
\end{bmatrix}
\end{equation*}
\begin{align*}
& L & \text{: element length} & & & & \\
& E & \text{: elastic modulus} & & & G & \text{: shear modulus} \\
& A & \text{: section area} & & & J & \text{: tortional constant} \\
& I_y & \text{: moment of inertia arounf y-axis} & & & I_z & \text{: moment of inertia around z-axis}
\end{align*}
座標変換行列
部材軸(x軸)の方向余弦
- 1つの梁要素の節点を $i$ および $j$ とする.
- 節点 $i$ の座標を, $(x_i,y_i,z_i)$, 節点 $j$ の座標を $(x_j,y_j,z_j)$ とする.
- この時,部材軸(x軸)の方向余弦は以下の通り表現できる.
\begin{gather*}
l=\cfrac{x_j-x_i}{\ell} \qquad m=\cfrac{y_j-y_i}{\ell} \qquad n=\cfrac{z_j-z_i}{\ell} \\
\ell=\sqrt{(x_j-x_i)^2+(y_j-y_i)^2+(z_j-z_i)^2}
\end{gather*}
座標変換行列の小行列
$\boldsymbol{[t]}$ は,全体座標系を部材座標系に変換する座標変換行列 (12 x 12) の小行列 (3 x 3) である.
\begin{equation*}
\boldsymbol{\{x\}}=\boldsymbol{[t]}\boldsymbol{\{X\}}
\end{equation*}
ここに,
$\boldsymbol{\{x\}}$ は部材座標,
$\boldsymbol{\{X\}}$ は全体座標
である.
(1) 部材長軸(部材座標系x軸)が全体座標系Z軸と平行でない場合
\begin{equation*}
\boldsymbol{[t]}=
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\theta & \sin\theta \\
0 & -\sin\theta & \cos\theta
\end{bmatrix}
\cdot
\begin{bmatrix}
l & m & n \\
-\cfrac{m}{\sqrt{l^2+m^2}} & \cfrac{l}{\sqrt{l^2+m^2}} & 0 \\
-\cfrac{l \cdot n}{\sqrt{l^2+m^2}} & -\cfrac{m \cdot n}{\sqrt{l^2+m^2}} & \sqrt{l^2+m^2}
\end{bmatrix}
\qquad \text{($\theta$ : chord angle)}
\end{equation*}
(2) 部材長軸(部材座標系x軸)が全体座標系Z軸と平行な場合
この時,$x_j-x_i=0$,$y_j-y_i=0$ であり,$l=0$,$m=0$ であることから,$\boldsymbol{[t]}$を書き直す必要がある.
\begin{equation*}
\boldsymbol{[t]}=
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\theta & \sin\theta \\
0 & -\sin\theta & \cos\theta
\end{bmatrix}
\cdot
\begin{bmatrix}
0 & 0 & n \\
n & 0 & 0 \\
0 & 1 & 0
\end{bmatrix}
\qquad \text{($\theta$ : chord angle)}
\end{equation*}
座標変換行列
\begin{equation*}
\boldsymbol{[T]}=
\begin{bmatrix}
\boldsymbol{[t]} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{[t]} & \boldsymbol{0} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{0} & \boldsymbol{[t]} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} &\boldsymbol{[t]}
\end{bmatrix}
\end{equation*}
コードアングルが0の場合の全体座標系と部材座標系の関係
2次元弾性応力解析
有限要素式
節点変位計算式
\begin{equation}
[\boldsymbol{k}]\{\boldsymbol{u}\}=\{\boldsymbol{f}\}+\{\boldsymbol{f_t}\}+\{\boldsymbol{f_b}\}
\end{equation}
\begin{align}
&[\boldsymbol{k}]=t\cdot \int_A [\boldsymbol{B}]^T[\boldsymbol{D}][\boldsymbol{B}] dA \\
&\{\boldsymbol{f_t}\}=t\cdot \int_A [\boldsymbol{B}]^T[\boldsymbol{D}]\{\boldsymbol{\epsilon_0}\} dA \\
&\{\boldsymbol{f_b}\}=t\cdot\gamma\cdot \int_A [\boldsymbol{N}]^T [\boldsymbol{N}] dA \cdot \{\boldsymbol{w}\}
\end{align}
要素応力算定式
\begin{equation}
\{\boldsymbol{\sigma}\}=[\boldsymbol{D}]\{\boldsymbol{\epsilon}-\boldsymbol{\epsilon_0}\}
\end{equation}
節点変位計算式では,温度変化による項 $\{\boldsymbol{f_t}\}$ を荷重ベクトルに加えて変位を計算しているが,要素応力を求める際は,上式に示すように,節点変位から求めた歪から温度変化による歪を差し引く必要が有ることに注意が必要である.
節点変位ー任意位置ひずみ関係式
\begin{equation}
\{\boldsymbol{\epsilon}\}=[\boldsymbol{B}]\{\boldsymbol{u}\}
\end{equation}
節点変位ー任意位置歪算定式
\begin{equation}
\{\boldsymbol{v}\}=[\boldsymbol{N}]\{\boldsymbol{u}\}
\end{equation}
| $[\boldsymbol{k}]$ | : 要素剛性マトリックス |
| $\{\boldsymbol{u}\}$ | : 節点変位ベクトル |
| $\{\boldsymbol{f}\}$ | : 節点外力ベクトル |
| $\{\boldsymbol{f_t}\}$ | : 温度変化による節点力ベクトル |
| $\{\boldsymbol{f_b}\}$ | : 自重・地震加速度による節点ベクトル |
| $[\boldsymbol{D}]$ | : 応力ー歪関係マトリックス |
| $t$, $\gamma$ | : 要素厚さ,要素単位体積重量 |
| $\{\boldsymbol{w}\}$ | : 節点加速度ベクトル(重力加速度に対する比率で入力) |
| $\{\boldsymbol{\epsilon_0}\}$ | : 温度変化による歪 |
| $\{\boldsymbol{\epsilon}\}$ | : 要素内任意点の歪 |
| $\{\boldsymbol{v}\}$ | : 要素内任意点の変位 |
2次元弾性問題における応力-ひずみ関係
一般に3次元問題における等方均質弾性体の応力-ひずみ関係は,弾性係数を$E$,ポアソン比を$\nu$,材料の線膨張係数を$\alpha$,温度変化量を$T$として以下の通りとなる(Hookeの法則).
\begin{equation}
\epsilon_x-\alpha T=\cfrac{1}{E}[\sigma_x-\nu(\sigma_y+\sigma_z)] \qquad
\epsilon_y-\alpha T=\cfrac{1}{E}[\sigma_y-\nu(\sigma_z+\sigma_x)] \qquad
\epsilon_z-\alpha T=\cfrac{1}{E}[\sigma_z-\nu(\sigma_x+\sigma_y)]
\end{equation}
\begin{equation}
\gamma_{xy}=\cfrac{2(1+\nu)}{E}\tau_{xy} \qquad
\gamma_{yz}=\cfrac{2(1+\nu)}{E}\tau_{yz} \qquad
\gamma_{zx}=\cfrac{2(1+\nu)}{E}\tau_{zx}
\end{equation}
ここで$x-y$平面上を考える場合,平面応力状態では,
\begin{equation}
\sigma_z=0 \qquad \tau_{yz}=0 \qquad \tau_{zx}=0
\end{equation}
であるため,
\begin{gather}
\epsilon_x-\alpha T=\cfrac{1}{E}(\sigma_x-\nu\sigma_y) \qquad
\epsilon_y-\alpha T=\cfrac{1}{E}(\sigma_y-\nu\sigma_x) \qquad
\gamma_{xy}=\cfrac{2(1+\nu)}{E}\tau_{xy} \\
\Longrightarrow
\begin{Bmatrix} \sigma_x \\ \sigma_y \\ \tau_{xy} \end{Bmatrix}
=\frac{E}{1-\nu^2}\begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & \cfrac{1-\nu}{2} \end{bmatrix}
\begin{Bmatrix} \epsilon_x-\alpha T \\ \epsilon_y-\alpha T \\ \gamma_{xy} \end{Bmatrix}
\end{gather}
平面ひずみ状態では,
\begin{equation}
\epsilon_z=0 \rightarrow \sigma_z=\nu(\sigma_x+\sigma_y)-E\alpha T \qquad \tau_{yz}=0 \qquad \tau_{zx}=0
\end{equation}
であるため,
\begin{gather}
\epsilon_x-\alpha T=\cfrac{1}{E}[(1-\nu^2)\sigma_x-\nu(1+\nu)\sigma_y] \qquad
\epsilon_y-\alpha T=\cfrac{1}{E}[(1-\nu^2)\sigma_y-\nu(1+\nu)\sigma_x] \qquad
\gamma_{xy}=\cfrac{2(1+\nu)}{E}\tau_{xy} \\
\Longrightarrow
\begin{Bmatrix} \sigma_x \\ \sigma_y \\ \tau_{xy} \end{Bmatrix}
=\frac{E}{(1+\nu)(1-2\nu)}\begin{bmatrix} 1-\nu & \nu & 0 \\ \nu & 1-\nu & 0 \\ 0 & 0 & \cfrac{1-2\nu}{2} \end{bmatrix}
\begin{Bmatrix} \epsilon_x-(1+\nu)\alpha T \\ \epsilon_y-(1+\nu)\alpha T \\ \gamma_{xy} \end{Bmatrix}
\end{gather}
となる.これらの関係を再整理すると以下の通りとなる.
2次元問題での応力とひずみの成分
\begin{equation}
\text{応力成分:}\{\boldsymbol{\sigma}\}=\begin{Bmatrix} \sigma_{x} \\ \sigma_{y} \\ \tau_{xy} \end{Bmatrix} \qquad
\text{ひずみ成分:}\{\boldsymbol{\epsilon}\}=\begin{Bmatrix} \epsilon_{x} \\ \epsilon_{y} \\ \gamma_{xy} \end{Bmatrix}
\end{equation}
\begin{align}
&\text{平面応力温度ひずみ成分:}\{\boldsymbol{\epsilon_0}\}=\begin{Bmatrix} \alpha T \\ \alpha T \\ 0 \end{Bmatrix} \\
&\text{平面ひずみ温度ひずみ成分:}\{\boldsymbol{\epsilon_0}\}=\begin{Bmatrix} (1+\nu)\alpha T \\ (1+\nu)\alpha T \\ 0 \end{Bmatrix}
\end{align}
応力・ひずみの符号は,引張を正とし,温度の符号は温度上昇を正とする.
2次元問題での応力-ひずみ関係式
\begin{equation}
\text{平面応力:}[\boldsymbol{D_e}]=\frac{E}{1-\nu^2}\begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & \cfrac{1-\nu}{2} \end{bmatrix} \qquad
\begin{matrix} E & \text{:弾性係数} \\ \nu & \text{:ポアソン比} \end{matrix}
\end{equation}
\begin{equation}
\text{平面ひずみ:}[\boldsymbol{D_e}]=\frac{E}{(1+\nu)(1-2\nu)}\begin{bmatrix} 1-\nu & \nu & 0 \\ \nu & 1-\nu & 0 \\ 0 & 0 & \cfrac{1-2\nu}{2} \end{bmatrix}
\end{equation}
4節点4ガウス積分点パラメトリック要素としての定式化
ひずみ-変位関係行列$[\boldsymbol{B}]$の導入
四角形要素内任意点の変位$u$,$v$を以下のように仮定する.ここに座標($a$,$b$)は[$-1$,$1$]の範囲を有する正規化パラメータ座標,$u_{i,j,k,l}$および$v_{i,j,k,l}$は要素を構成する節点の変位を示す.
\begin{align}
u=&N_1(a,b)\cdot u_i+N_2(a,b)\cdot u_j+N_3(a,b)\cdot u_k+N_4(a,b)\cdot u_l \\
v=&N_1(a,b)\cdot v_i+N_2(a,b)\cdot v_j+N_3(a,b)\cdot v_k+N_4(a,b)\cdot v_l
\end{align}
要素内任意点の変位を$\{\boldsymbol{u}\}$,節点変位を$\{\boldsymbol{u_{nd}}\}$とすれば,
\begin{equation}
\{\boldsymbol{u}\}=\begin{Bmatrix} u \\ v \end{Bmatrix}
=\begin{bmatrix}
N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4 & 0 \\
0 & N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4
\end{bmatrix}
\begin{Bmatrix}
u_i \\ v_i \\ u_j \\ v_j \\ u_k \\ v_k \\ u_l \\ v_l
\end{Bmatrix}
=[\boldsymbol{N}]\{\boldsymbol{u_{nd}}\}
\end{equation}
要素内任意点のひずみ$\{\boldsymbol{\epsilon}\}$は,節点変位$\{\boldsymbol{u_{nd}}\}$を用いて,
\begin{equation}
\{\boldsymbol{\epsilon}\}=\begin{Bmatrix} \cfrac{\partial u}{\partial x} \\ \cfrac{\partial v}{\partial y} \\ \cfrac{\partial u}{\partial y}+\cfrac{\partial v}{\partial x} \end{Bmatrix}
=\begin{bmatrix}
\cfrac{\partial N_1}{\partial x} & 0 & \cfrac{\partial N_2}{\partial x} & 0 & \cfrac{\partial N_3}{\partial x} & 0 & \cfrac{\partial N_4}{\partial x} & 0 \\
0 & \cfrac{\partial N_1}{\partial y} & 0 & \cfrac{\partial N_2}{\partial y} & 0 & \cfrac{\partial N_3}{\partial y} & 0 & \cfrac{\partial N_4}{\partial y} \\
\cfrac{\partial N_1}{\partial y} & \cfrac{\partial N_1}{\partial x} & \cfrac{\partial N_2}{\partial y} & \cfrac{\partial N_2}{\partial x} & \cfrac{\partial N_3}{\partial y} & \cfrac{\partial N_3}{\partial x} & \cfrac{\partial N_4}{\partial y} & \cfrac{\partial N_4}{\partial x}
\end{bmatrix}
\begin{Bmatrix}
u_i \\ v_i \\ u_j \\ v_j \\ u_k \\ v_k \\ u_l \\ v_l
\end{Bmatrix}
=[\boldsymbol{B}]\{\boldsymbol{u_{nd}}\}
\end{equation}
要素剛性行列
4節点パラメトリック要素の剛性行列$[\boldsymbol{k}]$は,要素の板厚を一定値$t$とし,応力-ひずみ関係行列を$[\boldsymbol{D_e}]$とすれば以下の通りとなる.
\begin{equation}
[\boldsymbol{k}]=t\int_{-1}^{1}\int_{-1}^{1}[\boldsymbol{B}]^{T}[\boldsymbol{D_e}][\boldsymbol{B}]\cdot\det(J)\cdot da\cdot db
=t\cdot \sum_{kk=1}^4 \left\{[\boldsymbol{B}]^{T}[\boldsymbol{D_e}][\boldsymbol{B}]\cdot\det(J)\right\}_{kk}
\end{equation}
温度変化による節点力ベクトル
温度変化によるひずみ$\{\boldsymbol{\epsilon_0}\}$による節点力ベクトル$\{\boldsymbol{f_t}\}$は以下の通りとなる.
\begin{equation}
\{\boldsymbol{f_t}\}=t\int_{-1}^{1}\int_{-1}^{1}[\boldsymbol{B}]^{T}[\boldsymbol{D_e}]\{\boldsymbol{\epsilon_0}\}\cdot\det(J)\cdot da\cdot db
=t\cdot \sum_{kk=1}^4 \left\{[\boldsymbol{B}]^{T}[\boldsymbol{D_e}]\{\boldsymbol{\epsilon_0}\}\cdot\det(J)\right\}_{kk}
\end{equation}
温度変化によるひずみの成分は以下のとおりである.
\begin{equation}
T_p=N_1\cdot\phi_i+N_2\cdot\phi_j+N_3\cdot\phi_k+N_4\cdot\phi_l
\end{equation}
\begin{align}
\text{平面応力:}&\{\boldsymbol{\epsilon_0}\}=\begin{Bmatrix} \alpha T_p \\ \alpha T_p \\ 0 \end{Bmatrix}
\\
\text{平面ひずみ:}&\{\boldsymbol{\epsilon_0}\}=\begin{Bmatrix} (1+\nu)\alpha T_p \\ (1+\nu)\alpha T_p \\ 0 \end{Bmatrix}
\end{align}
ここに,$\alpha$は線膨張係数,$\nu$はポアソン比,$T_p$は要素任意点の温度変化量,$\{\phi_i~~\phi_j~~\phi_k~~\phi_l\}^T$は節点温度変化量,$[N_1~~N_2~~N_3~~N_4]$は$[\boldsymbol{N}]$の要素である.また,温度変化量の符号は,温度上昇を正とする.
物体力による節点力ベクトル
要素内任意点に作用する物体力(ここでは慣性力とする)$\{\boldsymbol{F}\}=\{F_{Bx},F_{By}\}^T$は物体力に関わる節点力ベクトル$\{w\}$と内挿関数$[\boldsymbol{N}]$を用い以下の通り表せる.
\begin{equation}
\{\boldsymbol{F}\}=[\boldsymbol{N}]\{\boldsymbol{w}\}
\end{equation}
\begin{equation}
[\boldsymbol{N}]=\begin{bmatrix}N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4 & 0\\ 0 & N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4\end{bmatrix}
\end{equation}
\begin{equation}
\{\boldsymbol{w}\}=\gamma\cdot\begin{Bmatrix}k_h & k_v & k_h & k_v & k_h & k_v & k_h & k_v \end{Bmatrix}^T
\end{equation}
ここに$\gamma$は要素の単位体積重量(質量$\times$重力加速度),$k_h$および$k_v$は水平方向・鉛直方向の慣性力の係数(重力加速度に対する比率)である.
以上より,物体力(慣性力)による等価節点外力ベクトル$\{\boldsymbol{f_b}\}$は,
\begin{equation}
\{\boldsymbol{f_b}\}=t\cdot\int_{A}[\boldsymbol{N}]^T\{\boldsymbol{F}\}dA
=t\cdot\gamma\cdot\int_{A}[\boldsymbol{N}]^T[\boldsymbol{N}]dA\cdot\{\boldsymbol{w'}\}
=t\cdot\gamma\cdot\sum_{kk=1}^4 \left\{[\boldsymbol{N}]^T[\boldsymbol{N}]\cdot\det(J)\right\}_{kk}\cdot\{\boldsymbol{w'}\}
\end{equation}
として算定できる.ここでベクトル$\{\boldsymbol{w}\}$については$\gamma$をくくり出すととにより,
\begin{equation}
\{\boldsymbol{w'}\}=\begin{Bmatrix}k_h & k_v & k_h & k_v & k_h & k_v & k_h & k_v \end{Bmatrix}^T
\end{equation}
とおいている.
軸対称弾性応力解析
軸対称問題における応力-ひずみ関係とひずみ-変位関係
回転軸方向の応力・ひずみを添字$z$,半径方向の応力・ひずみを添字$r$,円周方向の応力・ひずみを添字$\theta$により表すとすれば,軸対称問題における応力-ひずみ関係式は,以下の通りとなる.
\begin{equation}
\begin{cases}
\epsilon_z-\alpha T=\cfrac{1}{E}\{\sigma_z-\nu(\sigma_r+\sigma_{\theta})\} \\
\epsilon_r-\alpha T=\cfrac{1}{E}\{\sigma_r-\nu(\sigma_z+\sigma_{\theta})\} \\
\epsilon_{\theta}-\alpha T=\cfrac{1}{E}\{\sigma_{\theta}-\nu(\sigma_z+\sigma_r)\} \\
\gamma_{zr}=\cfrac{2(1+\nu)}{E}\cdot\tau_{zr}
\end{cases}
\end{equation}
ここに,$\nu$はポアソン比,$\alpha$は熱膨張率,$T$は温度変化量である.
上式を変形することにより
\begin{equation}
\begin{cases}
\sigma_z=\cfrac{E}{(1+\nu)(1-2\nu)}\{(1-\nu)\epsilon_z+\nu\epsilon_r+\nu\epsilon_{\theta}-(1+\nu)\alpha T\} \\
\sigma_r=\cfrac{E}{(1+\nu)(1-2\nu)}\{\nu\epsilon_z+(1-\nu)\epsilon_r+\nu\epsilon_{\theta}-(1+\nu)\alpha T\} \\
\sigma_{\theta}=\cfrac{E}{(1+\nu)(1-2\nu)}\{\nu\epsilon_z+\nu\epsilon_r+(1-\nu)\epsilon_{\theta}-(1+\nu)\alpha T\} \\
\tau_{zr}=\cfrac{E}{2(1+\nu)}\cdot\gamma_{zr}
\end{cases}
\end{equation}
これを,マトリックスおよびベクトルの形で表せば以下の通りとなる.
\begin{equation}
\{\boldsymbol{\sigma}\}=[\boldsymbol{D_e}]\{\boldsymbol{\epsilon-\epsilon_0}\}
\end{equation}
\begin{equation}
\{\boldsymbol{\sigma}\}=\begin{Bmatrix} \sigma_z \\ \sigma_r \\ \sigma_{\theta} \\ \tau_{zr} \end{Bmatrix} \qquad
\{\boldsymbol{\epsilon}\}=\begin{Bmatrix} \epsilon_z \\ \epsilon_r \\ \epsilon_{\theta} \\ \gamma_{zr} \end{Bmatrix} \qquad
\{\boldsymbol{\epsilon_0}\}=\begin{Bmatrix} \alpha T \\ \alpha T \\ \alpha T \\ 0 \end{Bmatrix}
\end{equation}
\begin{equation}
[\boldsymbol{D_e}]=\cfrac{E}{(1+\nu)(1-2\nu)}\begin{bmatrix}
1-\nu & \nu & \nu & 0 \\
\nu & 1-\nu & \nu & 0 \\
\nu & \nu & 1-\nu & 0 \\
0 & 0 & 0 & \cfrac{1-2\nu}{2}
\end{bmatrix}
\end{equation}
回転軸方向の変位および半径方向の変位を,それぞれ$w$,$u$とおけば,ひずみ-変位関係式は以下の通りとなる.
\begin{equation}
\{\boldsymbol{\epsilon}\}
=\begin{Bmatrix} \epsilon_z \\ \epsilon_r \\ \epsilon_{\theta} \\ \gamma_{zr} \end{Bmatrix}
=\begin{Bmatrix} \cfrac{\partial w}{\partial z} \\ \cfrac{\partial u}{\partial r} \\ \cfrac{u}{r} \\ \cfrac{\partial w}{\partial r}+\cfrac{\partial u}{\partial z} \end{Bmatrix}
\end{equation}
4節点4ガウス積分点パラメトリック要素としての定式化
ひずみ-変位関係行列$[\boldsymbol{B}]$の導入
軸対称要素内任意点の回転軸方向変位$w$および半径方向変位$u$を以下のように仮定する.ここに座標$(a,b)$は$[-1,1]$の範囲を有する正規化パラメータ座標,$w_{i,j,k,l}$および$u_{i,j,k,l}$は要素を構成する節点の変位を示す.
\begin{align}
w=&N_1(a,b)\cdot w_i+N_2(a,b)\cdot w_j+N_3(a,b)\cdot w_k+N_4(a,b)\cdot w_l \\
u=&N_1(a,b)\cdot u_i+N_2(a,b)\cdot u_j+N_3(a,b)\cdot u_k+N_4(a,b)\cdot u_l
\end{align}
要素内任意点の変位を$\{\boldsymbol{u}\}$,節点変位を$\{\boldsymbol{u_{nd}}\}$とすれば,
\begin{equation}
\{\boldsymbol{u}\}=\begin{Bmatrix} w \\ u \end{Bmatrix}
=\begin{bmatrix}
N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4 & 0 \\
0 & N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4
\end{bmatrix}
\begin{Bmatrix}
w_i \\ u_i \\ w_j \\ u_j \\ w_k \\ u_k \\ w_l \\ u_l
\end{Bmatrix}
=[\boldsymbol{N}]\{\boldsymbol{u_{nd}}\}
\end{equation}
要素内任意点のひずみ$\{\boldsymbol{\epsilon}\}$は,節点変位$\{\boldsymbol{u_{nd}}\}$を用いて,
\begin{equation}
\{\boldsymbol{\epsilon}\}=\begin{Bmatrix} \cfrac{\partial w}{\partial z} \\ \cfrac{\partial u}{\partial r} \\ \cfrac{u}{r} \\ \cfrac{\partial w}{\partial r}+\cfrac{\partial u}{\partial z} \end{Bmatrix}
=\begin{bmatrix}
\cfrac{\partial N_1}{\partial z} & 0 & \cfrac{\partial N_2}{\partial z} & 0 & \cfrac{\partial N_3}{\partial z} & 0 & \cfrac{\partial N_4}{\partial z} & 0 \\
0 & \cfrac{\partial N_1}{\partial r} & 0 & \cfrac{\partial N_2}{\partial r} & 0 & \cfrac{\partial N_3}{\partial r} & 0 & \cfrac{\partial N_4}{\partial r} \\
0 & \cfrac{N_1}{r} & 0 & \cfrac{N_2}{r} & 0 & \cfrac{N_3}{r} & 0 & \cfrac{N_4}{r} \\
\cfrac{\partial N_1}{\partial r} & \cfrac{\partial N_1}{\partial z} & \cfrac{\partial N_2}{\partial r} & \cfrac{\partial N_2}{\partial z} & \cfrac{\partial N_3}{\partial r} & \cfrac{\partial N_3}{\partial z} & \cfrac{\partial N_4}{\partial r} & \cfrac{\partial N_4}{\partial z}
\end{bmatrix}
\begin{Bmatrix}
w_i \\ u_i \\ w_j \\ u_j \\ w_k \\ u_k \\ w_l \\ u_l
\end{Bmatrix}
=[\boldsymbol{B}]\{\boldsymbol{u_{nd}}\} \label{eq:axisym-4}
\end{equation}
要素内任意点の$r$座標値は,以下により評価する.
\begin{equation}
r=N_1\cdot r_i+N_2\cdot r_j+N_3\cdot r_k+N_4\cdot r_l
\end{equation}
ここに,$r_i$,$r_j$,$r_k$,$r_l$は要素を構成する節点の$r$座標値である.
要素剛性行列
要素剛性行列は,本来要素の体積積分により求めますが,棒や平面問題では簡略化し1次元積分や2次元積分を計算することによりこれらを求めている.軸対称要素の場合を考えてみると,回転中心より半径$r$の位置にある微小要素の体積は,$r\times d\theta\times dr\times dz$となる.ここで積分値や荷重ベクトルなどを,円周方向は1ラジアンで評価することとし,Gauss積分を用いるための積分変数変換を行えば,
\begin{equation}
r\times d\theta\times dr\times dz=r\times dr\times dz=r\times \det(J)\times da\times db
\end{equation}
となる.よって,軸対称要素における要素剛性行列$[\boldsymbol{k}]$は,応力-ひずみ関係行列を$[\boldsymbol{D_e}]$とすれば以下の通りとなる.
\begin{equation}
[\boldsymbol{k}]=\int_{-1}^{1}\int_{-1}^{1}[\boldsymbol{B}]^{T}[\boldsymbol{D_e}][\boldsymbol{B}]\cdot r \cdot\det(J)\cdot da\cdot db
=\sum_{kk=1}^4 \left\{[\boldsymbol{B}]^{T}[\boldsymbol{D_e}][\boldsymbol{B}]\cdot r \cdot\det(J)\right\}_{kk}
\end{equation}
2次元飽和-不飽和浸透流解析
2次元定常飽和浸透流問題の有限要素式
ダルシーの法則が成立する2次元直交異方性材料の直交座標系$x$-$y$における定常飽和浸透流問題の支配方程式は以下の通りである.なお奥行き方向の厚さは考慮しないことにする.
\begin{equation}
k_x\frac{\partial^2 \phi}{\partial x^2}+k_y\frac{\partial^2 \phi}{\partial y^2}=0 \label{eq:seep1}
\end{equation}
| $\phi$:全水頭 | $k_x$:$x$方向透水係数 | $k_y$:$y$方向透水係数 |
ここで,Galerkin法により,任意の$\delta \phi$に対し,支配方程式のの弱形式である次式を満足する未知数$\phi$を決定することを考える.
\begin{equation}
\int_A\delta \phi\left(k_x\frac{\partial^2 \phi}{\partial x^2}+k_y\frac{\partial^2 \phi}{\partial y^2}\right)dA=0
\end{equation}
有限要素において,要素内の任意箇所の全水頭$\phi$が,内挿関数行列$[\boldsymbol{N}]$(ただし1行$\times$節点自由度数列)と節点全水頭ベクトル$\{\boldsymbol{h}\}$を用いて,
\begin{equation}
\phi(x,y)=[\boldsymbol{N}(x,y)]\{\boldsymbol{h}\}
\end{equation}
と表せれば,
\begin{equation}
\{\boldsymbol{\delta h}\}^T\int_A [\boldsymbol{N}]^T \left(k_x\frac{\partial^2 \phi}{\partial x^2}+k_y\frac{\partial^2 \phi}{\partial y^2}\right)dA=0
\end{equation}
となるが,$\{\boldsymbol{\delta h}\}$は任意の節点水頭ベクトルであるため,面積積分値が0となる必要がある.
次に部分積分公式
\begin{equation}
f\cdot g'=(f\cdot g)'-f'\cdot g
\end{equation}
およびGreenの公式
\begin{equation}
\iint_D\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)dA=\int_C \left(P\frac{\partial x}{\partial n}+Q\frac{\partial y}{\partial n}\right)ds
\end{equation}
を用いることにより,
\begin{align}
0=&\int_A [\boldsymbol{N}]^T \left(k_x\frac{\partial^2 \phi}{\partial x^2}+k_y\frac{\partial^2 \phi}{\partial y^2}\right)dA \\
=&\int_A
\left\{
k_x\left(
\frac{\partial \left([\boldsymbol{N}]^T\frac{\partial \phi}{\partial x}\right)}{\partial x}-\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial \phi}{\partial x}
\right)
+k_y\left(
\frac{\partial \left([\boldsymbol{N}]^T\frac{\partial \phi}{\partial y}\right)}{\partial y}-\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial \phi}{\partial y}
\right)
\right\}
dA \\
=&\int_s [\boldsymbol{N}]^T \left(k_x\frac{\partial \phi}{\partial x}\frac{\partial x}{\partial n}+k_y\frac{\partial \phi}{\partial y}\frac{\partial y}{\partial n}\right)ds
-\int_A\left(k_x\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+k_y\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)dA\cdot\{\boldsymbol{h}\}
\end{align}
また,$x$方向および$y$方向の流速をそれぞれ$v_x$,$v_y$とすれば,ダルシーの法則より
\begin{equation}
v_x=-k_x\frac{\partial \phi}{\partial x} \qquad v_y=-k_x\frac{\partial \phi}{\partial y}
\end{equation}
以上により,要素有限要素式は以下の通り表現できる.
\begin{align}
&[\boldsymbol{k}]\{\boldsymbol{h}\}=\{\boldsymbol{q}\} \\
&[\boldsymbol{k}]=\int_A \left(k_x\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+k_y\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)dA \\
&\{\boldsymbol{q}\}=-\int_s [\boldsymbol{N}]^T \left(v_x \frac{\partial x}{\partial n}+v_y \frac{\partial y}{\partial n}\right)ds
\end{align}
| $[\boldsymbol{k}]$:透水性マトリックス | $\{\boldsymbol{h}\}$:節点全水頭ベクトル | $\{\boldsymbol{q}\}$:節点流量ベクトル |
なお$\{\boldsymbol{q}\}$は流速ベクトルの境界長さでの積分であり,流量を示すことは容易に理解できる.
4節点4ガウス積分点要素としての定式化
透水性マトリックス
面積積分の積分点を4点,線積分の積分点を2点とすれば,重みは1となるため,それぞれの行列・ベクトルは積分点での計算値の総和として次のように示される.
\begin{align}
[\boldsymbol{k}]=&\int_A \left(k_x\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+k_y\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)dA \\
=&\int_{-1}^{1}\int_{-1}^{1} \left(k_x\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+k_y\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)\cdot \det(J)\cdot da\cdot db \\
=&\sum_{kk=1}^{4} \left(k_x\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+k_y\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)\cdot \det(J) \\
\end{align}
節点流量ベクトル$\{\boldsymbol{q}\}$については,等価節点ベクトルとして直接入力すればよい.
要素内平均流速
要素内任意点の全水頭$\phi$は内挿関数$[\boldsymbol{N}]$と節点全水頭ベクトル$\{\boldsymbol{h}\}$を用いて
\begin{equation}
\phi=[\boldsymbol{N}]\{\boldsymbol{h}\}
\end{equation}
であることから,ダルシーの法則より要素内任意点の流速$v_x$および$v_y$は
\begin{align}
&v_x=-k_x\frac{\partial \phi}{\partial x} =-k_x\frac{\partial [\boldsymbol{N}]}{\partial x}\{\boldsymbol{h}\} \\
&v_y=-k_y\frac{\partial \phi}{\partial y} =-k_y\frac{\partial [\boldsymbol{N}]}{\partial y}\{\boldsymbol{h}\}
\end{align}
要素内平均流速は,要素内の4つのGauss積分点の平均とすればよいため,以下の通り求められる.
\begin{align}
&v_x=-\frac{k_x}{4}\sum_{kk=1}^{4}\left(\frac{\partial [\boldsymbol{N}]}{\partial x}\{\boldsymbol{h}\}\right) \\
&v_y=-\frac{k_y}{4}\sum_{kk=1}^{4}\left(\frac{\partial [\boldsymbol{N}]}{\partial y}\{\boldsymbol{h}\}\right)
\end{align}
注意:以上は異方性地盤を対象とした展開であるが,プログラムでは,等方性地盤のみを扱える
不飽和浸透流解析への拡張
飽和浸透流解析
飽和定常浸透流解析は,以下の連立一次方程式を解く問題となる.
\begin{equation*}
[k]\{h\}=\{q\}
\end{equation*}
\begin{equation*}
\begin{bmatrix}k_{11} & k_{12} & \dots \\
k_{21} & k_{22} & \dots \\
\dots & \dots & \dots \\
\dots & \dots & k_{nn}\end{bmatrix}
\begin{Bmatrix}h_{\text{unknown}} \\ h_{\text{unknown}} \\ \dots \\ h_{\text{given}} \end{Bmatrix}
=
\begin{Bmatrix}q_{\text{given}} \\ q_{\text{given}} \\ \dots \\ q_{\text{unknown}} \end{Bmatrix}
\end{equation*}
ここで,$\{q\}$は節点流量ベクトル,$\{h\}$は全水頭ベクトル,$[k]$は透水行列であり,以下の特性を有する.
- 透水行列$[k]$は定数,
- 節点流量ベクトル$\{q\}$の既知成分に相当する全水頭ベクトル$\{h\}$は未知数
- 節点流量ベクトル$\{q\}$の未知成分に相当する全水頭ベクトル$\{h\}$は既知数
このため,既知数と未知数の関係の処理を行った後,一回連立方程式を解くことにより解が得られる.
飽和-不飽和浸透流解析
飽和-不飽和浸透流解析での連立方程式は,以下の特性を有する.
- 境界条件には,流量既知,全水頭既知,浸潤面が出現する境界の3種類を考慮する必要がある.
- 浸潤面が出現する境界以外は,流量か全水頭のいずれかが既知となる.
- 浸潤面が出現する境界上では流量・全水頭とも未知数となる.
- ただし浸潤面が出現する境界は,基本的に大気に接する境界であるため,雨の流入などを考慮しなければ流量は流出のみ(プログラム上は0以下),
圧力水頭も0以下という制約がある.
- 飽和領域での透水行列の成分は定数であるが,不飽和領域での透水行列の成分はサクション圧(負の圧力水頭)の関数となっている.このため,収束計算により,未知数を定める必要がある.
収束計算の方法は,全節点に全水頭の初期値を与え,得られた解を次の収束計算の入力値とする,逐次代入法を用いている.この方法では全節点の水頭を仮定するため,仮定した水頭から全要素の透水行列を設定できるため,計算フローを単純化できるメリットがある.
全水頭の初期値は,全水頭既知境界以外は,飽和領域の最小全水頭を与える(要素領域の Z 座標の最小値)のが,解の精度・収束性を考慮したうえで有効のようである.
不飽和透水特性(van Genuchten モデル)
地盤の不飽和透水特性モデルは,飽和度-サクション圧関係,飽和度-不飽和透水係数比をテーブルで入力する方法もあるが,解析上,連続関数で取り扱うほうが,プログラムが単純化できるため,以下に示す van Genuchten モデルを採用している.
\begin{align}
&S_e=\left\{\frac{1}{1+\left(\alpha\cdot h_s\right)^n}\right\}^m \qquad\qquad n=\frac{1}{1-m} \quad & (0 < m < 1) \\
&K_r=(S_e)^{0.5}\cdot\left\{1-\left(1-S_e{}^{1/m}\right)^m\right\}^2 & (0 \leqq S_r, K_r \leqq 1) \\
&K=K_r \cdot K_0
\end{align}
| $S_e$ | Degree of saturation |
| $K_r$ | Relative hydraulic conductivity function |
| $h_s$ | Suction head (positive sign) |
| $\alpha$ | Scaling parameter |
| $m$ | Non-dimensional parameter |
| $K$ | Permiability coefficient |
| $K_0$ | Saturated permiability coefficient |
2次元非定常熱伝導解析
2次元非定常熱伝導問題の有限要素式
2次元等方性材料の直交座標系$x$-$y$における非定常熱伝導問題の支配方程式は以下の通りである.なお奥行き方向厚さは考慮しないことにする.
\begin{equation}
\rho c\frac{\partial T}{\partial t}=\kappa\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right)+\dot{Q}
\end{equation}
| $T$ | :温度 | $t$ | :時間 | $\dot{Q}$ | :発熱率 |
| $\rho$ | :密度 | $c$ | :比熱 | $\kappa$ | :熱伝導率 |
また,境界での熱流束$q$は,Fourierの法則より,境界上の外向き法線を$n$として,以下の通りとなる.
\begin{equation}
q=-\kappa\frac{\partial T}{\partial n}
\end{equation}
ここで,Galerkin法により,任意の$\delta T$に対し,支配方程式の弱形式である次式を満足する未知数$T$を決定することを考える.
\begin{equation}
\int_A\delta T\left\{\kappa\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right)+\dot{Q}-\rho c\frac{\partial T}{\partial t}\right\}dA=0
\end{equation}
有限要素において,要素内の任意箇所の温度$T$が,内挿関数行列$[\boldsymbol{N}]$(ただし1行$\times$節点自由度数列)と節点温度ベクトル$\{\boldsymbol{\phi}\}$を用いて,
\begin{equation}
T(x,y,t)=[\boldsymbol{N}(x,y)]\{\boldsymbol{\phi}(t)\}
\end{equation}
と表せれば,
\begin{equation}
\{\boldsymbol{\delta\phi}\}^T\int_A [\boldsymbol{N}]^T \left\{\kappa\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right)+\dot{Q}-\rho c\frac{\partial T}{\partial t}\right\}dA=0
\end{equation}
となるが,$\{\boldsymbol{\delta\phi}\}$は任意の節点温度ベクトルであるため,面積積分値が0となることが必要となる.
次に部分積分公式
\begin{equation}
f\cdot g'=(f\cdot g)'-f'\cdot g
\end{equation}
およびGreenの公式
\begin{equation}
\iint_D\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)dA=\int_C \left(P\frac{\partial x}{\partial n}+Q\frac{\partial y}{\partial n}\right)ds
\end{equation}
およびFourierの法則を用いることにより,$\kappa$に係る項は,
\begin{align}
&\int_A [\boldsymbol{N}]^T \left\{\kappa\left(\frac{\partial^2 h}{\partial x^2}+\frac{\partial^2 h}{\partial y^2}\right)\right\}dA \\
=&\int_A \kappa
\left\{
\left(
\frac{\partial \left([\boldsymbol{N}]^T\frac{\partial h}{\partial x}\right)}{\partial x}-\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial h}{\partial x}
\right)
+\left(
\frac{\partial \left([\boldsymbol{N}]^T\frac{\partial h}{\partial y}\right)}{\partial y}-\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial h}{\partial y}
\right)
\right\}
dA \\
=&
\int_s [\boldsymbol{N}]^T \kappa \left(\frac{\partial h}{\partial x}\frac{\partial x}{\partial n}+\frac{\partial h}{\partial y}\frac{\partial h}{\partial x}\right)ds
-\int_A \kappa \left(\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)dA\cdot\{\boldsymbol{\phi}\} \\
=&
-\int_s q[\boldsymbol{N}]^T ds
-\int_A \kappa \left(\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)dA \cdot\{\boldsymbol{\phi}\}
\end{align}
また
\begin{equation}
\int_A [\boldsymbol{N}]^T \left(\dot{Q}-\rho c \frac{\partial T}{\partial t}\right)dA
=\int_A \dot{Q}[\boldsymbol{N}]^T dA-\int_A \rho c [\boldsymbol{N}]^T [\boldsymbol{N}]dA \cdot \left\{\frac{\partial \boldsymbol{\phi}}{\partial t}\right\}
\end{equation}
以上により,要素有限要素式は以下の通り表現できる.
\begin{align}
&[\boldsymbol{k}]\{\boldsymbol{\phi}\}+[\boldsymbol{c}]\left\{\cfrac{\partial \boldsymbol{\phi}}{\partial t}\right\}=\{\boldsymbol{f}\} \\
&[\boldsymbol{k}]=\int_A \kappa\left(\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)dA \\
&[\boldsymbol{c}]=\int_A \rho c [\boldsymbol{N}]^T [\boldsymbol{N}]dA \\
&\{\boldsymbol{f}\}=\int_A \dot{Q}[\boldsymbol{N}]^T dA-\int_s q[\boldsymbol{N}]^T ds
\end{align}
| $[\boldsymbol{k}]$ | :熱伝導マトリックス | $[\boldsymbol{c}]$ | :熱容量マトリックス |
| $\{\boldsymbol{\phi}\}$ | :節点温度ベクトル | $\{\boldsymbol{f}\}$ | :熱流束ベクトル |
境界条件に関する補足
境界(要素の辺)で熱流束$q_0$が与えられている場合は
\begin{equation}
\int_s q[\boldsymbol{N}]^T ds=\int_s q_0 [\boldsymbol{N}]^T ds
\end{equation}
とおけばよく,断熱境界では$q_0=0$とおけばよいことになる.
境界(要素の辺)で熱伝達がある場合は,熱伝達率を$\alpha_c$,境界温度を$T_c$として
\begin{align}
\int_s q[\boldsymbol{N}]^T ds=&\int_s \alpha_c (T-T_c) [\boldsymbol{N}]^T ds \\
=&\int_s \alpha_c[\boldsymbol{N}]^T [\boldsymbol{N}]ds\cdot \{\boldsymbol{\phi}\}-\int_s\alpha_c T_c[\boldsymbol{N}]^T ds
\end{align}
となり,それぞれの成分を熱伝導マトリックスおよび熱流束ベクトルに足し込む必要がある.
境界条件を考慮した熱伝導マトリックス・熱流束ベクトルによる有限要素式
\begin{equation}
[\boldsymbol{k}]\{\boldsymbol{\phi}\}+[\boldsymbol{c}]\left\{\cfrac{\partial \boldsymbol{\phi}}{\partial t}\right\}=\{\boldsymbol{f}\}
\end{equation}
\begin{align}
&[\boldsymbol{k}]=\int_A \kappa\left(\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)dA
+\int_s \alpha_c[\boldsymbol{N}]^T [\boldsymbol{N}]ds \\
&[\boldsymbol{c}]=\int_A \rho c [\boldsymbol{N}]^T [\boldsymbol{N}]dA \\
&\{\boldsymbol{f}\}=\int_A \dot{Q}[\boldsymbol{N}]^T dA+\int_s \alpha_c T_c [\boldsymbol{N}]^T ds
\end{align}
| $[\boldsymbol{k}]$ | : 熱伝導マトリックス.第2項は熱伝達境界によるもの |
| $[\boldsymbol{c}]$ | : 熱容量マトリックス |
| $\{\boldsymbol{\phi}\}$ | : 節点温度ベクトル |
| $\{\boldsymbol{f}\}$ | : 熱流束ベクトル.第1項は発熱によるもの,第2項は熱伝達によるもの |
| $[\boldsymbol{N}]$ | : 内挿関数行列 |
| $\kappa$, $\rho$, $c$ | : 熱伝導率,密度,比熱 |
| $\alpha_c$, $T_c$ | : 熱伝達率,熱伝達境界の外部温度 |
| $\dot{Q}$ | : 発熱率 |
| $\int_A$, $\int_S$ | : 要素面積および要素辺での積分 |
発熱体に関する補足説明
セメント・コンクリートをモデルとした発熱体を扱えます.セメント.コンクリートの断熱温度上昇量を,以下の式で仮定する.
\begin{equation}
T=K\cdot(1-e^{-\alpha\cdot t})
\end{equation}
| $T$: 断熱温度上昇量 | $K$: 最高上昇温度 | $\alpha$: 発熱速度を示すパラメータ | $t$: 時間 |
上式の中の,$K$ (Tk) および $\alpha$ (Al) を材料特性として入力する.
上式を用い,発熱量 $Q$ および発熱率 $\dot{Q}$ は以下のように表現できる.
\begin{equation}
Q=\rho \cdot c \cdot T(t) \quad \rightarrow \quad \dot{Q}=\rho \cdot c \cdot T_k \cdot \alpha \cdot e^{-\alpha t}
\end{equation}
非定常有限要素式の解法
非定常有限要素式を解く上での時間離散化手法として,Crank-Nicolson差分式を用いる.
解析範囲全体の有限要素式を以下の通りとする.
\begin{equation}
[\boldsymbol{K}]\{\boldsymbol{\Phi}\}+[\boldsymbol{C}]\left\{\cfrac{\partial \boldsymbol{\Phi}}{\partial t}\right\}=\{\boldsymbol{F}\}
\end{equation}
ここで,時刻$t+\Delta t/2$での節点温度ベクトル$\{\boldsymbol{\Phi}\}$,節点温度ベクトル時間微分$\{\partial\boldsymbol{\Phi}/\partial t\}$,および節点熱流束ベクトル$\{\boldsymbol{F}\}$を以下の通りおきます.
\begin{align}
\left\{\boldsymbol{\Phi}\left(t+\frac{\Delta}{2}\right)\right\}=&\frac{\{\boldsymbol{\Phi}(t+\Delta t)\}+\{\boldsymbol{\Phi}(t)\}}{2} \\
\left\{\frac{\partial \boldsymbol{\Phi}}{\partial t}\left(t+\frac{\Delta}{2}\right)\right\}=&\frac{\{\boldsymbol{\Phi}(t+\Delta t)\}-\{\boldsymbol{\Phi}(t)\}}{\Delta t} \\
\left\{\boldsymbol{F}\left(t+\frac{\Delta}{2}\right)\right\}=&\frac{\{\boldsymbol{F}(t+\Delta t)\}+\{\boldsymbol{F}(t)\}}{2}
\end{align}
これらを,上述の解析範囲全体の有限要素式に代入することにより,以下の差分式が得られ,時刻$t$における既知ベクトルを用いて$t+\Delta t$における節点温度を逐次求めることができる.
\begin{equation}
\left(\frac{1}{2}[\boldsymbol{K}]+\frac{1}{\Delta t}[\boldsymbol{C}]\right)\{\boldsymbol{\Phi}(t+\Delta t)\}
=\left(-\frac{1}{2}[\boldsymbol{K}]+\frac{1}{\Delta t}[\boldsymbol{C}]\right)\{\boldsymbol{\Phi}(t)\}+\frac{\{\boldsymbol{F}(t+\Delta t)\}+\{\boldsymbol{F}(t)\}}{2}
\end{equation}
要素の材料特性は時間により変化しない設定をしているため,時間ステップ計算では,$numpy.linalg.inv(A)$ で一回だけ上式左辺の逆行列を求め,これを記憶して各時刻の温度履歴を計算している.
4節点4ガウス積分点要素としての定式化
面積積分の積分点を4点,線積分の積分点を2点とすれば,重みは1となるため,それぞれの行列・ベクトルは積分点での計算値の総和として次のように示される.なお,次式中$\ell$は境界条件を指定された要素辺の実長を表す.
要素熱伝導マトリックス
\begin{align}
[\boldsymbol{k}]=&\int_A \kappa\left(\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)dA
+\int_s \alpha_c[\boldsymbol{N}]^T [\boldsymbol{N}]ds \\
=&\int_{-1}^{1}\int_{-1}^{1} \kappa\left(\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)\cdot \det(J)\cdot da\cdot db
+\frac{\ell}{2}\int_{-1}^{1} \alpha_c[\boldsymbol{N}]^T [\boldsymbol{N}]ds \\
=&\sum_{kk=1}^{4} \kappa\left(\frac{\partial [\boldsymbol{N}]^T}{\partial x}\frac{\partial [\boldsymbol{N}]}{\partial x}+\frac{\partial [\boldsymbol{N}]^T}{\partial y}\frac{\partial [\boldsymbol{N}]}{\partial y}\right)\cdot \det(J)
+\frac{\ell}{2}\sum_{kk=1}^{2} \alpha_c[\boldsymbol{N}]^T [\boldsymbol{N}] \\
\end{align}
要素熱容量マトリックス
\begin{align}
[\boldsymbol{c}]=&\int_A \rho c [\boldsymbol{N}]^T [\boldsymbol{N}]dA \\
=&\int_{-1}^{1}\int_{-1}^{1} \rho c [\boldsymbol{N}]^T [\boldsymbol{N}]\cdot \det(J)\cdot da\cdot db \\
=&\sum_{kk=1}^{4} \rho c [\boldsymbol{N}]^T [\boldsymbol{N}]\cdot \det(J) \\
\end{align}
熱流束ベクトル
\begin{align}
\{\boldsymbol{f}\}=&\int_A \dot{Q}[\boldsymbol{N}]^T dA+\int_s \alpha_c T_c [\boldsymbol{N}]^T ds-\int_s q_0[\boldsymbol{N}]^T ds \\
=&\int_{-1}^{1}\int_{-1}^{1}\dot{Q}[\boldsymbol{N}]^T\cdot \det(J)\cdot da\cdot db
+\frac{\ell}{2}\int_{-1}^{1} \alpha_c T_c[\boldsymbol{N}]^Tds
-\frac{\ell}{2}\int_{-1}^{1} q_0[\boldsymbol{N}]^T ds \\
=&\sum_{kk=1}^{4}\dot{Q}[\boldsymbol{N}]^T\cdot \det(J)
+\frac{\ell}{2}\sum_{kk=1}^{2} \alpha_c T_c[\boldsymbol{N}]^T
-\frac{\ell}{2}\sum_{kk=1}^{2} q_0[\boldsymbol{N}]^T
\end{align}
2次元弾性骨組構造振動解析
運動方程式とNermarkのβ法
単純化のため1質点系を考える.時刻$t+\Delta t$での質点系の釣り合いを示す運動方程式は以下の通り.ここにドットは時間微分を示す.
\begin{equation}
m\cdot\ddot{u}(t+\Delta t)+c\cdot\dot{u}(t+\Delta t)+k\cdot u(t+\Delta t)=f(t+\Delta t)
\end{equation}
| $m$ :質量 | $\ddot{u}$ :加速度 |
| $c$ :減衰係数 | $\dot{u}$ :速度 |
| $k$ :バネ定数 | $u$ :変位 |
| $f$ :外力 | |
時刻$t+\Delta t$での変位$u$および速度$\dot{u}$をTaylor展開したものを以下に示す.
\begin{align}
u(t+\Delta t)&=u(t)+\frac{\Delta t}{1!}\cdot\dot{u}(t)+\frac{(\Delta t)^2}{2!}\cdot\ddot{u}(t)+\frac{(\Delta t)^3}{3!}\cdot\dddot{u}(t)+\cdots \\
\dot{u}(t+\Delta t)&=\dot{u}(t)+\frac{\Delta t}{1!}\cdot\ddot{u}(t)+\frac{(\Delta t)^2}{2!}\cdot\dddot{u}(t)+\cdots
\end{align}
ここで,変位については右辺第4項において$1/3!=\beta$とおくことにより,速度については右辺第3項において$1/2!=\gamma$とおき,双方で高次項を無視することにより以下の式が得られる.
\begin{align}
u(t+\Delta t)&=u(t)+\Delta t\cdot\dot{u}(t)+\frac{(\Delta t)^2}{2}\cdot\ddot{u}(t)+\beta\cdot(\Delta t)^3\cdot\dddot{u}(t) \\
\dot{u}(t+\Delta t)&=\dot{u}(t)+\Delta t\cdot\ddot{u}(t)+\gamma\cdot(\Delta t)^2\cdot\dddot{u}(t)
\end{align}
次に,$\dddot{u}$を以下のように線形化する.
\begin{equation}
\dddot{u}(t)=\frac{\ddot{u}(t+\Delta t)-\ddot{u}(t)}{\Delta t}
\end{equation}
上記関係を用いて,運動方程式を整理することにより,以下の方程式が得られる.
\begin{align}
u(t+\Delta t)&=u(t)+\Delta t\cdot\dot{u}(t)+\left(\frac{1}{2}-\beta\right)(\Delta t)^2\cdot\ddot{u}(t)+\beta(\Delta t)^2\cdot\ddot{u}(t+\Delta t) \\
\dot{u}(t+\Delta t)&=\dot{u}(t)+(1-\gamma)\cdot\Delta t\cdot\ddot{u}(t)+\gamma\cdot\Delta t\cdot\ddot{u}(t+\Delta t)
\end{align}
ここで,有限要素法への適用を考えると,変位を未知数として方程式を解きたいため,加速度と速度を既知の値および時刻$t+\Delta t$での変位で表すよう式を変形する.
\begin{align}
&\ddot{u}(t+\Delta t)=\cfrac{1}{\beta (\Delta t)^2}\cdot\left[u(t+\Delta t)-u(t)\right]-\cfrac{1}{\beta\Delta t}\cdot\dot{u}(t)-\left(\cfrac{1}{2\beta}-1\right)\cdot\ddot{u}(t) \\
&\dot{u}(t+\Delta t)=\cfrac{\gamma}{\beta\Delta t}\cdot\left[u(t+\Delta t)-u(t)\right]-\left(\cfrac{\gamma}{\beta}-1\right)\cdot\dot{u}(t)-\left(\cfrac{\gamma}{2\beta}-1\right)\Delta t \cdot\ddot{u}(t)
\end{align}
上記を運動方程式に代入することにより,以下の関係が得られる.
\begin{align}
\left(\cfrac{1}{\beta(\Delta t)^2}\cdot m+\cfrac{\gamma}{\beta \Delta t}\cdot c+k\right)\cdot u(t+\Delta t) &= f(t+\Delta t) \\
&+ m\cdot\left[\cfrac{1}{\beta(\Delta t)^2}\cdot u(t)+\cfrac{1}{\beta \Delta t}\cdot \dot{u}(t)+\left(\cfrac{1}{2\beta}-1\right)\cdot \ddot{u}(t)\right] \\
&+ c\cdot\left[\cfrac{\gamma}{\beta\Delta t}\cdot u(t)+\left(\cfrac{\gamma}{\beta}-1\right)\cdot \dot{u}(t)+\left(\cfrac{\gamma}{2\beta}-1\right)\Delta t \cdot\ddot{u}(t)\right]
\end{align}
ここで通常は,$\gamma=1/2$ が用いられ,$\beta=1/4$とすれば平均加速度法,$\beta=1/6$とすれば線形加速度法となる.
マトリックス表示した解くべき方程式
1質点系で求めた上式を,$\gamma=1/2$に固定し,マトリックス表示すると以下の通りとなる.
変位算定式
\begin{equation}
\left(\frac{1}{\beta (\Delta t)^2}[\boldsymbol{m}]+\frac{1}{2\beta\Delta t}[\boldsymbol{c}]+[\boldsymbol{k}]\right)\{\boldsymbol{u}(t+\Delta t)\}=
\{\boldsymbol{f}(t+\Delta t)\}+[\boldsymbol{m}]\{\boldsymbol{w_a}(t)\}+[\boldsymbol{c}]\{\boldsymbol{w_b}(t)\}
\end{equation}
\begin{align}
&\{\boldsymbol{w_a}(t)\}=\frac{1}{\beta (\Delta t)^2}\{\boldsymbol{u}(t)\}+\frac{1}{\beta\Delta t}\{\boldsymbol{\dot{u}}(t)\}+\left(\frac{1}{2\beta}-1\right)\{\boldsymbol{\ddot{u}}(t)\} \\
&\{\boldsymbol{w_b}(t)\}=\frac{1}{2\beta\Delta t}\{\boldsymbol{u}(t)\}+\left(\frac{1}{2\beta}-1\right)\{\boldsymbol{\dot{u}}(t)\}+\left(\frac{1}{4\beta}-1\right)\Delta t\{\boldsymbol{\ddot{u}}(t)\}
\end{align}
変位速度・加速度算定式
上記により変位$\{\boldsymbol{u}(t+\Delta t)\}$を求めた後,下記のより変位速度$\{\boldsymbol{\dot{u}}(t+\Delta t)\}$,加速度$\{\boldsymbol{\ddot{u}}(t+\Delta t)\}$を求める.
\begin{align}
&\{\boldsymbol{\dot{u}}(t+\Delta t)\} =\frac{1}{2\beta\Delta t}\left(\{\boldsymbol{u}(t+\Delta t)\}-\{\boldsymbol{u}(t)\}\right)-\left(\frac{1}{2\beta}-1\right)\{\boldsymbol{\dot{u}}(t)\}-\left(\frac{1}{4\beta}-1\right)\Delta t\{\boldsymbol{\ddot{u}}(t)\} \\
&\{\boldsymbol{\ddot{u}}(t+\Delta t)\}=\frac{1}{\beta (\Delta t)^2}\left(\{\boldsymbol{u}(t+\Delta t)\}-\{\boldsymbol{u}(t)\}\right)-\frac{1}{\beta\Delta t}\{\boldsymbol{\dot{u}}(t)\}-\left(\frac{1}{2\beta}-1\right)\{\boldsymbol{\ddot{u}}(t)\}
\end{align}
| $[\boldsymbol{m}]$ :質量マトリックス | $\{\boldsymbol{\ddot{u}}\}$ :加速度ベクトル |
| $[\boldsymbol{c}]$ :減衰マトリックス | $\{\boldsymbol{\dot{u}}\}$ :速度ベクトル |
| $[\boldsymbol{k}]$ :剛性マトリックス | $\{\boldsymbol{u}\}$ :変位ベクトル |
| $\{\boldsymbol{f}\}$ :外力ベクトル | |
|
ここに,平均加速度法:$\beta=1/4$,線形加速度法:$\beta=1/6$である.
1質点系や多質点系においては,加速度を未知数として解く式をよく見かけるが,有限要素法への適用においては,非線形を取り入れる場合に有利であるなどの理由から,変位を未知数とする場合も多いようである.
また直感的に釣り合い式の表現は,$m\cdot a=f$か,$k\cdot u=f$ですが,筆者の直感的感覚は,有限要素法では$k\cdot u=f$であり,プログラムは変位を未知数として解くよう作成することにした.
剛性マトリックス・質量マトリックス
\begin{gather}
\{\boldsymbol{f_*}\}=[\boldsymbol{k}]\{\boldsymbol{u_*}\} \\
\{\boldsymbol{f_*}\}=\begin{Bmatrix} N_i & S_i & M_i & N_j & S_j & M_j \end{Bmatrix}^{T} \\
\{\boldsymbol{u_*}\}=\begin{Bmatrix} u_i & v_i & \theta_i & u_j & v_j & \theta_j \end{Bmatrix}^{T}
\end{gather}
\begin{equation}
[\boldsymbol{k}]=
\begin{bmatrix}
EA/\ell & 0 & 0 & -EA/\ell & 0 & 0 \\
0 & 12EI/\ell^3 & 6EI/\ell^2 & 0 & -12EI/\ell^3 & 6EI/\ell^2 \\
0 & 6EI/\ell^2 & 4EI/\ell & 0 & -6EI/\ell^2 & 2EI/\ell \\
-EA/\ell & 0 & 0 & EA/\ell & 0 & 0 \\
0 & -12EI/\ell^3 & -6EI/\ell^2 & 0 & 12EI/\ell^3 & -6EI/\ell^2 \\
0 & 6EI/\ell^2 & 2EI/\ell & 0 & -6EI/\ell^2 & 4EI/\ell
\end{bmatrix}
\end{equation}
\begin{equation}
[\boldsymbol{m}]=\frac{\gamma\cdot A \cdot \ell}{g}
\begin{bmatrix}
1/3 & 0 & 0 & 1/6 & 0 & 0 \\
0 & 13/35 & 11\ell/210 & 0 & 9/70 & -13\ell/420 \\
0 & 11\ell/210 & \ell^2/105 & 0 & 13\ell/420 & -\ell^2/140 \\
1/6 & 0 & 0 & 1/3 & 0 & 0 \\
0 & 9/70 & 13\ell/420 & 0 & 13/35 & -11\ell/210 \\
0 & -13\ell/420 & -\ell^2/140 & 0 & -11\ell/210 & \ell^2/105
\end{bmatrix}
\end{equation}
\begin{equation}
[\boldsymbol{T}]=
\begin{bmatrix}
\cos\phi & \sin\phi & 0 & 0 & 0 & 0 \\
-\sin\phi & \cos\phi & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & \cos\phi & \sin\phi & 0 \\
0 & 0 & 0 & -\sin\phi & \cos\phi & 0 \\
0 & 0 & 0 & 0 & 0 & 1
\end{bmatrix}
\end{equation}
| $\{\boldsymbol{f_*}\}$:要素節点力ベクトル | $E$:要素弾性係数 |
| $\{\boldsymbol{u_*}\}$:要素節点変位ベクトル | $A$:要素断面積 |
| $[\boldsymbol{k}]$ :要素剛性マトリックス | $I$:要素断面2次モーメント |
| $[\boldsymbol{m}]$ :要素質量マトリックス | $\ell$:要素長 |
| $[\boldsymbol{T}]$ :座標変換マトリックス | $\gamma$:要素単位体積重量 |
| $[\boldsymbol{T}]^T$ :転置を示す | $g$:重力加速度 |
座標変換マトリックス$[\boldsymbol{T}]$は,全体座標系変位を要素座標系変位に変換するものである.
全体座標系での剛性マトリックス$[\boldsymbol{K}]$と要素座標系での剛性マトリックス$[\boldsymbol{k}]$には次の関係がある.
\begin{equation}
[\boldsymbol{K}]=[\boldsymbol{T}]^T[\boldsymbol{k}][\boldsymbol{T}]
\end{equation}
全体座標系での質量マトリックス$[\boldsymbol{M}]$と要素座標系での質量マトリックス$[\boldsymbol{m}]$についても同様に次の関係がある.
\begin{equation}
[\boldsymbol{M}]=[\boldsymbol{T}]^T[\boldsymbol{m}][\boldsymbol{T}]
\end{equation}
減衰マトリックス
実際の計算で,構造物の減衰を考慮する場合,減衰マトリックス$[\boldsymbol{C}]$を具体的に与える必要がある.
ここでは,減衰マトリックスの与え方について考えてみる.
単純化のため地盤加速度を受ける1質点系の運動方程式を考える.
\begin{align}
&m\cdot\ddot{u}+c\cdot\dot{u}+k\cdot u=-m\cdot\ddot{\phi}\\
&\ddot{u}+\cfrac{c}{m}\cdot\dot{u}+\cfrac{k}{m}\cdot u=-\ddot{\phi}\\
&\ddot{u}+2\cdot h\cdot\omega\cdot\dot{u}+\omega^2\cdot u=-\ddot{\phi}
\end{align}
\begin{equation}
h=\cfrac{c/m}{2\cdot\omega} \qquad \omega=\sqrt{\cfrac{k}{m}}
\end{equation}
ここで,よく使われる減衰の形として,Rayleigh減衰を考える.これは,減衰係数は質量と剛性に比例するという考え方であり,以下の式表現となる.
\begin{equation}
c=\zeta_m\cdot m+\zeta_k\cdot k
\end{equation}
上式を考慮して減衰定数$h$を書き直してみると ($\omega$は固有円振動数,$f$は振動数)
\begin{equation}
h=\cfrac{c/m}{2\cdot\omega}=\cfrac{\zeta_m\cdot m+\zeta_k\cdot k}{2\cdot\omega\cdot m}
=\cfrac{\zeta_m}{2\cdot\omega}+\cfrac{\zeta_k\cdot\omega}{2}
=\cfrac{1}{4\pi f}\cdot\zeta_m+\pi f\cdot\zeta_k
\end{equation}
よって,もし現地測定などで,$i$次モードと$j$次モードの減衰定数$h_i$,$h_j$および固有振動数$f_i$,$f_j$が判れば,上式を連立させることにより,比例定数$\zeta_m$および$\zeta_k$を求めることができる.
\begin{equation}
\begin{cases}
h_i=\cfrac{1}{4\pi f_i}\cdot\zeta_m+\pi f_i\cdot\zeta_k \\
h_j=\cfrac{1}{4\pi f_j}\cdot\zeta_m+\pi f_j\cdot\zeta_k
\end{cases}
\quad\Longrightarrow
\begin{cases}
&\zeta_m=\cfrac{4\pi\cdot f_i\cdot f_j\cdot(f_j\cdot h_i-f_i\cdot h_j)}{f_j^2-f_i^2}\\
&\zeta_k=\cfrac{f_j\cdot h_j-f_i\cdot h_i}{\pi (f_j^2-f_i^2)}
\end{cases}
\end{equation}
減衰係数をマトリックス表示すれば,上記で定めたスカラー量$\zeta_m$および$\zeta_k$を用いて,
\begin{equation}
[\boldsymbol{C}]=\zeta_m\cdot[\boldsymbol{M}]+\zeta_k\cdot[\boldsymbol{K}]
\end{equation}
なお,実務上は比例定数の求め方として,以下のような手法が用いられる場合がある.
- 振動モードに応じた減衰定数がよくわからないので,減衰定数の値は1つとして,一般に使われている値(例えば$h_1=h_2=0.05$)などにセットする.
- 固有振動数については,固有値解析などで求めることができるため,1次および2次の固有振動数$f_1$,$f_2$を求める.
- 2つの固有振動数$f_1$,$f_2$と2つの減衰定数$h_1=h_2=0.05$が定まれば,上式により,比例定数$\zeta_m$および$\zeta_k$を求めることができる.
固有値解析
構造系の固有円振動数 $\omega$ をもとめるには,一般化固有値問題として,以下の固有方程式を解けば良い.
\begin{equation}
\left([\boldsymbol{K}]-\omega^2 [\boldsymbol{M}]\right) \{\boldsymbol{U}\} = \{\boldsymbol{0}\}
\end{equation}
固有円振動数 $\omega_n$ が求まれば,以下の関係により固有周期 $f_n$ を求めることができる.
\begin{equation}
f_n=\cfrac{\omega_n}{2 \pi}
\end{equation}
2次元弾性骨組構造幾何学的非線形解析
増分形剛性方程式
よく知られているように,幾何学的非線形項を含む増分形剛性方程式は,以下の通りとなる.
\begin{equation*}
\{\Delta f\}=[K_T]\{\Delta u\} \qquad [K_T]=[K_L]+[K_G]
\end{equation*}
\begin{align*}
&\{\Delta f\}=\begin{Bmatrix} \Delta N_i & \Delta S_i & \Delta M_i & \Delta N_j & \Delta S_j & \Delta M_j \end{Bmatrix}^T \\
&\{\Delta u\}=\begin{Bmatrix} \Delta u_i & \Delta v_i & \Delta \theta_i & \Delta u_j & \Delta v_j & \Delta \theta_j \end{Bmatrix}^T
\end{align*}
\begin{align*}
&[K_L]=
\begin{bmatrix}
EA/\ell & 0 & 0 & -EA/\ell & 0 & 0 \\
0 & 12EI/\ell^3 & 6EI/\ell^2 & 0 & -12EI/\ell^3 & 6EI/\ell^2 \\
0 & 6EI/\ell^2 & 4EI/\ell & 0 & -6EI/\ell^2 & 2EI/\ell \\
-EA/\ell & 0 & 0 & EA/\ell & 0 & 0 \\
0 & -12EI/\ell^3 & -6EI/\ell^2 & 0 & 12EI/\ell^3 & -6EI/\ell^2 \\
0 & 6EI/\ell^2 & 2EI/\ell & 0 & -6EI/\ell^2 & 4EI/\ell
\end{bmatrix}
\\
&[K_G]=P\cdot
\begin{bmatrix}
1/\ell & 0 & 0 & -1/\ell & 0 & 0 \\
0 & 6/5\ell & 1/10 & 0 & -6/5\ell & 1/10 \\
0 & 1/10 & 2\ell/15 & 0 & -1/10 & -\ell/30 \\
-1/\ell & 0 & 0 & 1/\ell & 0 & 0 \\
0 & -6/5\ell & -1/10 & 0 & 6/5\ell & -1/10 \\
0 & 1/10 & -\ell/30 & 0 & -1/10 & 2\ell/15
\end{bmatrix}
\end{align*}
| $[K_T]$ | : 要素接線剛性マトリックス |
| $[K_L]$ | : 要素線形剛性マトリックス |
| $[K_G]$ | : 要素幾何学的非線形剛性マトリックス |
| $P$ | : 要素軸力(引張が正) |
| $\{\Delta f\}$ | :要素節点力増分 |
| $\{\Delta u\}$ | :要素変位増分 |
| $E , A , I , \ell$ | : 弾性係数,断面積,断面2次モーメント,要素長 |
| $\Delta N , \Delta S , \Delta M$ | : 軸力増分,せん断力増分,モーメント増分 |
| $\Delta u , \Delta v , \Delta \theta$ | : 軸方向変位増分,軸直行方向変位増分,回転変位増分 |
| 添字 $i$,$j$ | : 節点$i$および節点$j$ |
内力計算
内力計算
内力増分 $\{\Delta f^*\}$ は,線形剛性マトリックス $[K_L]$ 及び剛体回転を除去した部材座標系での変位増分 $\{\Delta u^*\}$ から計算される.
\begin{equation*}
\{\Delta f^*\}=[K_L]\{\Delta u^*\}
\end{equation*}
\begin{align*}
&\{\Delta f^*\} =\begin{Bmatrix} \Delta N^*_i & \Delta S^*_i & \Delta M^*_i & \Delta N^*_j & \Delta S^*_j & \Delta M^*_j \end{Bmatrix}^T \\
&\{\Delta u^*\}=\begin{Bmatrix} \Delta u^*_i & \Delta v^*_i & \Delta \theta^*_i & \Delta u^*_j & \Delta v^*_j & \Delta \theta^*_j \end{Bmatrix}^T
\end{align*}
\begin{align*}
&\Delta u^*_i=0 &~& \Delta v^*_i=0 &~& \Delta \theta^*_i=(\tan\theta^*_i)_k-(\tan\theta^*_i)_{k-1} \\
&\Delta u^*_j=\Delta\ell & & \Delta v^*_j=0 & & \Delta \theta^*_j=(\tan\theta^*_j)_k-(\tan\theta^*_j)_{k-1}
\end{align*}
ここに, $\Delta\ell$ は収束計算中の前回と今回の要素長の変化を表す.
回転量についても,前回回転量(添字 $k-1$)と今回回転量(添字 $k$)が考慮される.
剛体回転の除去
剛体回転の除去方法を以下に示す.
正接加法定理を用いて,
\begin{align*}
&\frac{dv^*}{dx^*}|_i=\tan\theta^*_i=\tan(\theta_i-R)=\frac{\tan\theta_i-\tan R}{1+\tan\theta_i\tan R}
=\frac{(\ell+u_j-u_i)\tan\theta_i-(v_j-v_i)}{(\ell+u_j-u_i)+(v_j-v_i)\tan\theta_i} \\
&\frac{dv^*}{dx^*}|_j=\tan\theta^*_j=\tan(\theta_j-R)=\frac{\tan\theta_j-\tan R}{1+\tan\theta_j\tan R}
=\frac{(\ell+u_j-u_i)\tan\theta_j-(v_j-v_i)}{(\ell+u_j-u_i)+(v_j-v_i)\tan\theta_j} \\
&\left(\tan R=\frac{v_j-v_i}{\ell+u_j-u_i}, \quad \frac{dv}{dx}|_i=\tan\theta_i, \quad \frac{dv}{dx}|_j=\tan\theta_j \right)
\end{align*}
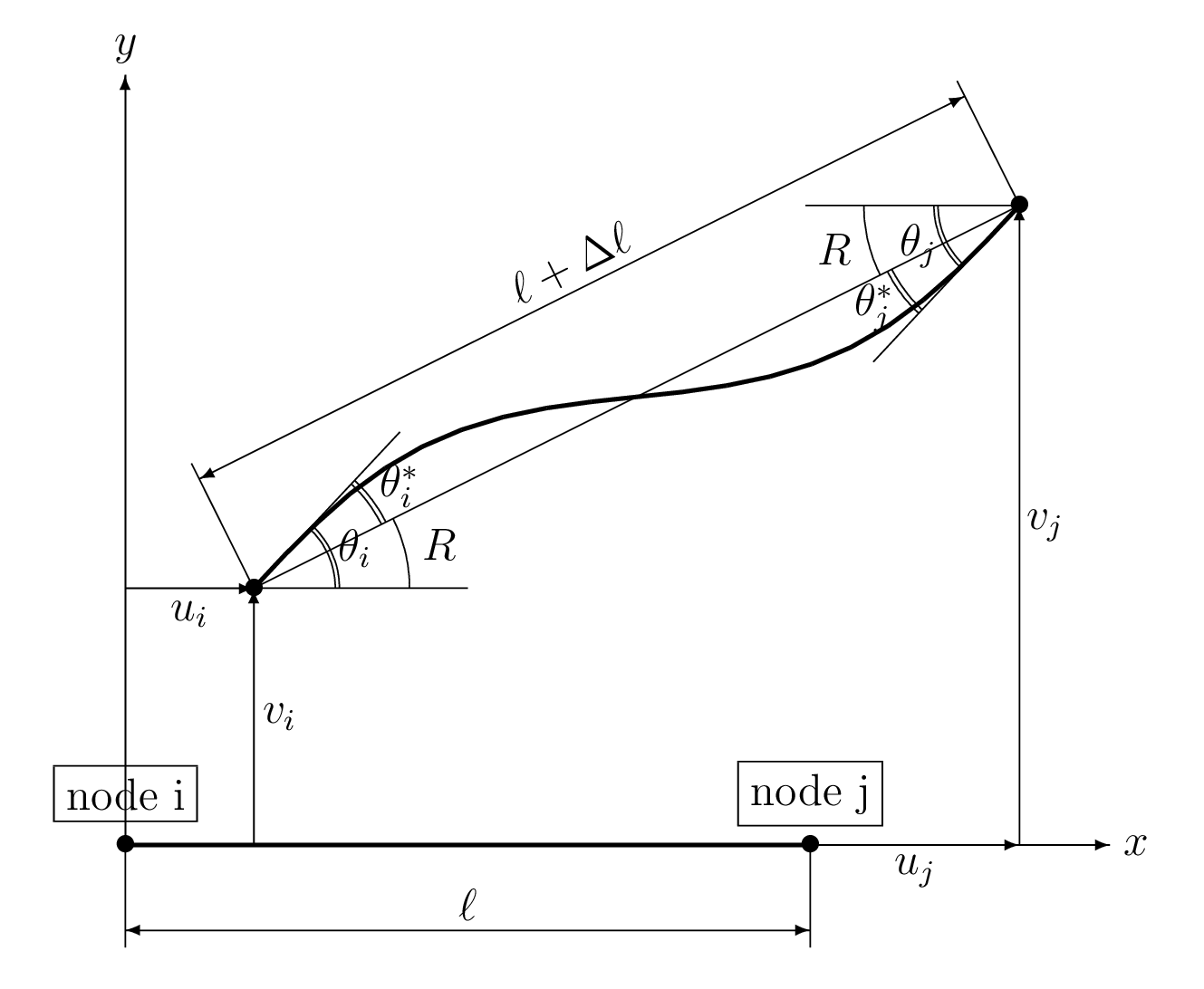 |
| Elimination of rigid rotation |
|---|
上式を用いて,現時点での $(\tan\theta_i^*)_k$, $(\tan\theta_j^*)_k$ および前回の
$(\tan\theta_i^*)_{k-1}$, $(\tan\theta_j^*)_{k-1}$ を計算できる.
これらから,以下のように,剛体回転を除去した回転量増分が計算できる.
\begin{align*}
&\Delta \theta^*_i=(\tan\theta^*_i)_k-(\tan\theta^*_i)_{k-1} \\
&\Delta \theta^*_j=(\tan\theta^*_j)_k-(\tan\theta^*_j)_{k-1}
\end{align*}
これらのステップでは,初期状態(変形前)の節点座標から計算した座標変換行列を用いる.
弧長法
図に示すような,単純化されたスカラー量の荷重-変位曲線を考える.
この図を参照して,以下の関係が導かれる.
\begin{align*}
K_T\cdot\Delta U=&\Delta\lambda\cdot\phi\Delta F+\Delta R \\
\Delta U=&\Delta\lambda\cdot\Delta U_0+\Delta U_R
\end{align*}
\begin{align*}
(\Delta s)^2&=(\Delta U)^2+(\Delta\lambda\cdot\phi\Delta F)^2 \\
&=(\Delta\lambda)^2\{(\Delta U_0)^2+(\phi\Delta F)^2\}+2\lambda\cdot(\Delta U_0\cdot\Delta U_R)+(\Delta U_R)^2
\end{align*}
\begin{equation*}
\Delta\lambda=\cfrac{-(\Delta U_0\cdot\Delta U_R)\pm\sqrt{\left\{(\Delta U_0)^2+(\phi\Delta F)^2)\right\}\cdot(\Delta s)^2-(\phi\Delta F\cdot\Delta U_R)^2}}{(\Delta U_0)^2+(\phi\Delta F)^2}
\end{equation*}
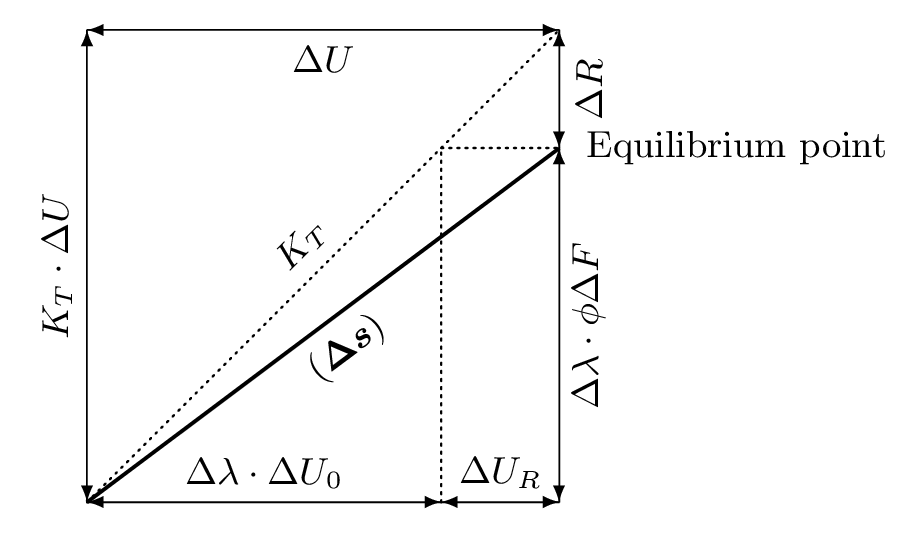 |
| Concept of Arc-Length method |
|---|
| ここに, | $K_T$ | : 接線剛性 | $\Delta\lambda$ | : 外力に乗じる係数 |
| | $\Delta F$ | : 外力増分 | $\Delta U_0$ | : 外力増分相当の変位増分 |
| | $\Delta R$ | : 不平衡力増分 | $\Delta U_R$ | : 不平衡力相当の変位増分 |
| | $\Delta U$ | : 変位増分 | $\Delta s$ | : 弧長 |
| | | | $\phi$ | : スケーリングパラメータ |
$\Delta\lambda$ の初期値
$\Delta U_R=0$ を仮定すれば,$\Delta\lambda$ は以下のように表せる.
\begin{equation*}
\Delta\lambda_0=\pm\sqrt{\frac{(\Delta s)^2}{(\Delta U_0)^2+(\phi\Delta F)^2}}
\end{equation*}
上式は,プラス・マイナスの2つの値を取り得る.また弧長法ではこの$\Delta\lambda_0$の符号が非常に重要になる.
$\Delta\lambda_0$ の符号は,以下のように定める.
- 前回釣り合い点から今回釣り合い点までの変位増分ベクトル ${\Delta U_{-1}}$ を定義する
- $\{\Delta U_0\}$ の計算($\{\Delta U_0\}=[K_T]^{-1}\{\Delta F\}$)
- 内積 $\{\Delta U_{-1}\}^T\{\Delta U_0\}=|\Delta U_{-1}|\cdot |\Delta U_0|\cdot \cos\theta$ の計算.ここで, $\theta$ は2つの変位ベクトルのなす角を示す.
- 内積が,$\{\Delta U_{-1}\}^T\{\Delta U_0\} \geqq 0$ なら,角度 $\theta$ は90度以下である.この場合,$\Delta\lambda_0$ の符号は正(プラス)とする.
- 内積が,$\{\Delta U_{-1}\}^T\{\Delta U_0\} \lt 0$ なら,角度 $\theta$ は90度より大きい.この場合,$\Delta\lambda_0$ の符号は負(マイナス)とする.
スケーリングパラメータ $\phi$ は,以下の式で計算する.このプログラムでは,
$\alpha=1.0$ としている.
\begin{equation*}
\phi=\sqrt{\frac{\alpha}{\{\Delta F\}^T\{\Delta F\}}}
\end{equation*}
弧長 $\Delta s$ は,$\Delta\lambda=1.0$ を仮定して以下の式で求める.
\begin{equation*}
\Delta s=\sqrt{\{\Delta U_0\}^T\{\Delta U_0\}+\phi^2\cdot\{\Delta F\}^T\{\Delta F\}} \qquad (\Delta\lambda_0=1.0)
\end{equation*}
収束計算のための補正係数 $\Delta\lambda$
前出の図を参照して, $\Delta s$ を $\Delta L$ に置き換えることにより,以下の式が得られる.
\begin{align*}
(\Delta L)^2&=(\Delta U)^2+(\Delta\lambda\cdot\phi\Delta F)^2 \\
&=(\Delta\lambda)^2\{(\Delta U_0)^2+(\phi\Delta F)^2\}+2\Delta\lambda\cdot(\Delta U_0\cdot\Delta U_R)+(\Delta U_R)^2
\end{align*}
上式の $(\Delta L)^2$ を最小化する条件より,$\Delta\lambda$ は以下のように計算できる.
\begin{equation*}
\frac{d(\Delta L)^2}{d\Delta\lambda}=0 \quad\rightarrow\quad \Delta\lambda=-\frac{\Delta U_0\cdot\Delta U_R}{(\Delta U_0)^2+(\phi\Delta F)^2}
\end{equation*}
解析のフローチャート
| $\{F\}$ | : 釣り合い点での全外力ベクトル |
| $\{\Delta F\}$ | : 外力増分べクロツ |
| $\{R\}$ | : 内力ベクトル |
| $\{\Delta R\}$ | : 不平衡力ベクトル |
| $\{U\}$ | : 全変位ベクトル |
| $\{\Delta U\}$ | : 変位増分ベクトル |
| $\{\Delta U_0\}$ | : 外力増分相当の変位増分ベクトル |
| $\{\Delta U_R\}$ | : 不平衡力相当の変位増分ベクトル |
| $\{\Delta U_{-1}\}$ | : 前回釣り合い点から今回釣り合い点までの変位増分ベクトル |
| $[K_T]$ | : 非線形項を含む接線剛性マトリックス |
| $\Delta s$ | : 弧長 |
| $\lambda$ | : 外力増分・変位増分に対する係数 |
| $\Delta\lambda$ | : 係数 $\lambda$ の増分 |
| $\phi$ | : スケーリングパラメータ |
 |
| Flowchart of Calculation |
|---|
実際のプログラムでは, $\Delta s$ と $\Delta\lambda$ は以下のような扱いとなっている.
- 初期載荷重(nnn=1)において, $\Delta s$ を計算し,また $\Delta\lambda_0=1.0$ にセットする.
- もし計算された $\Delta\lambda$ が $\Delta\lambda_0$ と比較して非常に小さい場合, $\Delta s$ は増加させる必要がある.なぜならば $\Delta s$ は $\Delta\lambda=1.0$ を仮定して計算されているからである.
- もし計算された $\Delta\lambda$ が初期の $\Delta\lambda_0 (=1.0)$ より大きければ,$\Delta s$ の増加はストップされる.なぜならば過大な $\Delta s$ は,予期せぬ挙動を引き起こす原因になるからである.
# Initial parameter setting for Arc-length method
if nnn==1:
ds0=np.sqrt(np.sum(dis0*dis0)+spara*spara*np.sum(df*df))
ds=ds0
dlam0=1.0
dlam=np.sqrt(ds*ds/(np.sum(dis0*dis0)+spara*spara*np.sum(df*df)))
if np.abs(dlam) < 0.1*np.abs(dlam0): ds=ds*1.2
if np.abs(dlam0) < np.abs(dlam): ds=ds
dlam=np.sqrt(ds*ds/(np.sum(dis0*dis0)+spara*spara*np.sum(df*df)))
if np.sum(dis_ref*dis0)<0.0: dlam=-dlam
2次元弾性骨組構造座屈解析
固有方程式
座屈荷重および変形モードを求めるための固有方程式は,以下のとおりである.
$[K_L]$および$[K_G]$は,幾何学的非線形解析に用いるものと同じ形であるが,$[K_G]$に含まれる軸力$P$について,座屈解析では圧縮を正とするところに注意が必要である.
下記固有方程式を解くことにより係数$\lambda$が求まるが,$[K_G]$に含まれる軸力$P$を確定する必要があるため,単位の荷重を入力して,固有値解析の前に,線形解析を1回実施しておく必要がある.
\begin{equation*}
\left\{[K_L]-\lambda [K_G]\right\}\{u\}=\{0\}
\end{equation*}
\begin{align*}
&[K_L]=
\begin{bmatrix}
EA/\ell & 0 & 0 & -EA/\ell & 0 & 0 \\
0 & 12EI/\ell^3 & 6EI/\ell^2 & 0 & -12EI/\ell^3 & 6EI/\ell^2 \\
0 & 6EI/\ell^2 & 4EI/\ell & 0 & -6EI/\ell^2 & 2EI/\ell \\
-EA/\ell & 0 & 0 & EA/\ell & 0 & 0 \\
0 & -12EI/\ell^3 & -6EI/\ell^2 & 0 & 12EI/\ell^3 & -6EI/\ell^2 \\
0 & 6EI/\ell^2 & 2EI/\ell & 0 & -6EI/\ell^2 & 4EI/\ell
\end{bmatrix}
\\
&[K_G]=P\cdot
\begin{bmatrix}
1/\ell & 0 & 0 & -1/\ell & 0 & 0 \\
0 & 6/5\ell & 1/10 & 0 & -6/5\ell & 1/10 \\
0 & 1/10 & 2\ell/15 & 0 & -1/10 & -\ell/30 \\
-1/\ell & 0 & 0 & 1/\ell & 0 & 0 \\
0 & -6/5\ell & -1/10 & 0 & 6/5\ell & -1/10 \\
0 & 1/10 & -\ell/30 & 0 & -1/10 & 2\ell/15
\end{bmatrix}
\end{align*}
| $[K_L]$ | : 要素線形剛性マトリックス |
| $[K_G]$ | : 要素幾何学的非線形剛性マトリックス |
| $P$ | : 要素軸力(圧縮が正) |
| $\{u\}$ | :要素変位 |
| $E , A , I , \ell$ | : 弾性係数,断面積,断面2次モーメント,要素長 |
| 添字 $i$,$j$ | : 節点$i$および節点$j$ |
1次元非定常熱伝導解析
非定常有限要素式の解法
2次元非定常熱伝導解析と同様,Crank-Nicolson 差分式に有限要素式を当てはめた結果は,以下のとおりである.
\begin{equation}
\left(\frac{1}{2}[\boldsymbol{K}]+\frac{1}{\Delta t}[\boldsymbol{C}]\right)\{\boldsymbol{\Phi}(t+\Delta t)\}
=\left(-\frac{1}{2}[\boldsymbol{K}]+\frac{1}{\Delta t}[\boldsymbol{C}]\right)\{\boldsymbol{\Phi}(t)\}+\frac{\{\boldsymbol{F}(t+\Delta t)\}+\{\boldsymbol{F}(t)\}}{2}
\end{equation}
| $[\boldsymbol{K}]$ | :熱伝導マトリックス | $[\boldsymbol{C}]$ | :熱容量マトリックス |
| $\{\boldsymbol{\Phi}\}$ | :節点温度ベクトル | $\{\boldsymbol{F}\}$ | :熱流束ベクトル |
それぞれのマトリックス・ベクトルを,要素単位で示すと以下の通りとなる.
\begin{align}
&[\boldsymbol{k}]=\cfrac{\kappa\cdot A}{\ell}
\begin{bmatrix}
1 & -1 \\
-1 & 1
\end{bmatrix}
+\alpha_{ci}\cdot A
\begin{bmatrix}
1 & 0 \\
0 & 0
\end{bmatrix}
+\alpha_{cj}\cdot A
\begin{bmatrix}
0 & 0 \\
0 & 1
\end{bmatrix}
\\
&[\boldsymbol{c}]=\rho \cdot c \cdot \ell \cdot A
\begin{bmatrix}
1/3 & 1/6 \\
1/6 & 1/3
\end{bmatrix}
\\
&\{\boldsymbol{f}\}=\cfrac{\dot{Q}\cdot\ell\cdot A}{2} \begin{Bmatrix} 1 \\ 1 \end{Bmatrix}
+\alpha_{ci}\cdot T_{ci}\cdot A \begin{Bmatrix} 1 \\ 0 \end{Bmatrix}
+\alpha_{cj}\cdot T_{cj}\cdot A \begin{Bmatrix} 0 \\ 1 \end{Bmatrix}
\end{align}
| $\kappa$ | :要素熱伝導率 | $c$ | :要素比熱 | $\rho$ | :要素密度 |
| $\ell$ | :要素長 | $A$ | :要素断面積 | $\dot{Q}$ | :要素発熱率 |
| $\alpha_{ci}$ | :節点$i$の熱伝達率(熱伝達境界でなければ$\alpha_{ci}=0$) |
| $\alpha_{ci}$ | :節点$j$の熱伝達率(熱伝達境界でなければ$\alpha_{cj}=0$) |
| $T_i$ | :節点$i$の熱伝達境界外部温度 |
| $T_j$ | :節点$i$の熱伝達境界外部温度 |
発熱体に関する説明
セメント・コンクリートをモデルとした発熱体を扱える.セメント.コンクリートの断熱温度上昇量を,以下の式で仮定している.
\begin{equation}
T=K\cdot(1-e^{-\alpha\cdot t})
\end{equation}
| $T$: 断熱温度上昇量 | $K$: 最高上昇温度 | $\alpha$: 発熱速度を示すパラメータ | $t$: 時間 |
上式の中の,$K$ (Tk) および $\alpha$ (Al) を材料特性として入力する.
上式を用い,発熱量 $Q$ および発熱率 $\dot{Q}$ は以下のように表現できる.
\begin{equation}
Q=\rho \cdot c \cdot T(t) \quad \rightarrow \quad \dot{Q}=\rho \cdot c \cdot T_k \cdot \alpha \cdot e^{-\alpha t}
\end{equation}