Contents
岩盤の内圧負担モデル
水圧鉄管における岩盤負担設計モデルの概要を下図に示す.水圧鉄管の岩盤負担設計式は,以下の仮定により導かれた弾性理論式である.
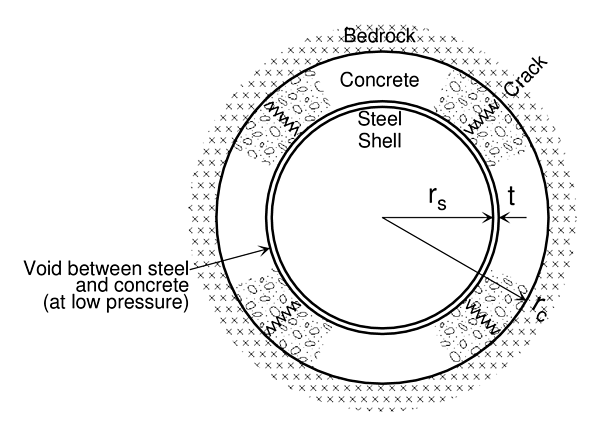 |
| Model of Penstock for Pressure Sharing Design by Bedrock |
|---|
| Item | Description |
|---|
| 水圧鉄管 | 円周方向応力のみを負担する弾性体. |
| 充填コンクリート | ひび割れ発生を考慮し,半径方向圧縮力のみを伝える弾性体とする.
ただし鉄管背面間隙量評価のため塑性変形係数を導入. |
| 岩盤 | 十分な初期地圧の存在を前提に,円周方向・半径方向の引張・圧縮応力を伝える無限弾性体とする.
ただしコンクリートと同様に鉄管背面間隙量評価のため塑性変形係数を導入.
なお実務設計では,掘削面周辺は緩みを考慮し,弾性係数の低下および引張応力を伝達しないとする場合もある. |
| 鉄管背面間隙 | コンクリート・岩盤の塑性変形,鉄管の温度降下,コンクリートの硬化収縮により低水圧時に発生する間隙を考慮. |
| 基礎方程式 | 内水圧による鉄管の半径方向変位量が,鉄管背面間隙量およびコンクリートおよび岩盤の圧縮変位量の和に等しいとして設計式を導出. |
記号の定義
| $t$ | 鉄管板厚 | | $\delta_s$ | 鉄管の半径方向弾性変形量 |
| $r_s$ | 鉄管内半径 | | $\delta_c$ | コンクリートの半径方向弾性変形量 |
| $r_c$ | トンネル掘削内半径 | | $\delta_g$ | 岩盤の半径方向弾性変形量 |
| $P$ | 設計内圧 | | $\delta_0$ | 鉄管背面間隙量 |
| $P_s$ | 鉄管の負担する内圧 | | $\Delta_c$ | コンクリートの塑性変形量 |
| $\lambda$ | 岩盤の内圧負担率 | | $\Delta_g$ | 岩盤の塑性変形量 |
| $\Delta T$ | 鉄管の温度変化量 | | $\Delta_s$ | 鉄管の温度降下による間隙量 |
| $\alpha_s$ | 鉄管の線膨張係数 | | $\Delta_{sd}$ | コンクリートの硬化収縮量 |
| $E_s$ | 鉄管の弾性係数 | | $\sigma_s$ | 鉄管の円周方向応力 |
| $E_c$ | コンクリートの弾性係数 | | $\sigma_c$ | コンクリートの半径方向応力 |
| $E_g$ | 岩盤の弾性係数 | | $\sigma_r$ | 岩盤の半径方向応力 |
| $m_g$ | 岩盤のポアソン数($=1/\nu_g$) | | $\sigma_{\theta}$ | 岩盤の円周方向応力 |
| $\nu_g$ | 岩盤のポアソン比 | | $\varepsilon_s$ | 鉄管の円周方向ひずみ |
| $\beta_c$ | コンクリートの塑性変形係数 | | $\varepsilon_c$ | コンクリートの半径方向ひずみ |
| $\beta_g$ | 岩盤の塑性変形係数 | | $\varepsilon_g$ | 岩盤の半径方向ひずみ |
| $D$ | 鉄管内径 | | $\sigma_{sa}$ | 鉄管許容応力 |
| $D_R$ | トンネル掘削径 | | | |
基礎方程式
鉄管,コンクリート,岩盤の変形量を以下の通り定義する.鉄管の内水圧による弾性変形量 $\delta_s$ は,コンクリート・岩盤の圧縮弾性変形量 $\delta_c~,~\delta_g$ および鉄管背面間隙量 $\delta_0$ の総和に等しいものとして,
\begin{equation}
\delta_s=\delta_c+\delta_g+\delta_0 \tag{1}
\end{equation}
また,鉄管背面間隙量 $\delta_0$ (初期充水以降)は,コンクリート・岩盤の塑性変形量 $\Delta_c~,~\Delta_g$ ,鉄管の温度降下による間隙量 $\Delta_s$ およびコンクリートの硬化収縮量 $\Delta_{sd}$ の総和に等しいものとして,
\begin{equation}
\delta_0=\Delta_c+\Delta_g+\Delta_s+\Delta_{sd} \tag{2}
\end{equation}
さらに,鉄管の負担する内圧 $P_s$ は,設計内圧 $P$ および岩盤の内圧負担率 $\lambda$ により,以下の通り表されるものとする.
\begin{equation}
P_s=P(1-\lambda) \tag{3}
\end{equation}
構造体の弾性変形量
鉄管の弾性変形量
鉄管の板厚は構造系全体の寸法と比較して小さいので,鉄管を円周方向応力のみを伝える薄肉円筒と考える.微小中心角 $\Delta\theta$ の鉄管要素の力の釣り合いより,
\begin{equation}
2\sigma_s\sin\left(\frac{\Delta\theta}{2}\right)\cdot t=P_s\cdot r_s\cdot\Delta\theta
\end{equation}
ここで $\Delta\theta$ は微小であるため,
\begin{equation}
2\sigma_s\left(\frac{\Delta\theta}{2}\right)\cdot t=P_s\cdot r_s\cdot\Delta\theta
\end{equation}
よって,鉄管の円周方向応力は,
\begin{equation}
\sigma_s=\frac{P_s\cdot r_s}{t} \tag{4}
\end{equation}
また,鉄管の円周方向ひずみは,
\begin{equation}
\varepsilon_s=\frac{\Delta_s}{r_s}
\end{equation}
よって,鉄管の変形量は,
\begin{equation}
\delta_s=r_s\cdot\varepsilon_s=r_s\frac{\sigma_s}{E_s}=\frac{P_s\cdot r_s^2}{E_s\cdot t} \tag{5}
\end{equation}
コンクリートの弾性変形量
鉄管の変形によりコンクリートには円周方向の引張力および半径方向の圧縮力が作用するが,コンクリートは圧縮力のみを伝達するとし,コンクリート内の任意の半径 $r$ における力の釣り合いより,
\begin{equation}
2\pi r\sigma_c=2\pi r_s(P-P_s)
\end{equation}
\begin{equation}
\sigma_c=\frac{(P-P_s)r_s}{r} \qquad \text{(圧縮応力)} \tag{6}
\end{equation}
よって,コンクリートのひずみは,圧縮を正として,
\begin{equation}
\varepsilon_c=\frac{\sigma_c}{E_c}=\frac{(P-P_s)r_s}{E_c\cdot r}
\end{equation}
コンクリートの変形量は,コンクリートのひずみをコンクリート厚で積分したものとなるため,
\begin{equation}
\delta_c=\int_{r_s}^{r_c}\varepsilon_c dr=\int_{r_s}^{r_c}\frac{(P-P_s)r_s}{E_c\cdot r}dr=\frac{(P-P_s)r_s}{E_c}\ln\left(\frac{r_c}{r_s}\right) \tag{7}
\end{equation}
岩盤の弾性変形量
岩盤には,初期地圧が作用しているため,鉄管から伝わる内圧に対しては,圧縮応力となる半径方向応力および引張応力となる円周方向応力ともに伝達できるものとする.
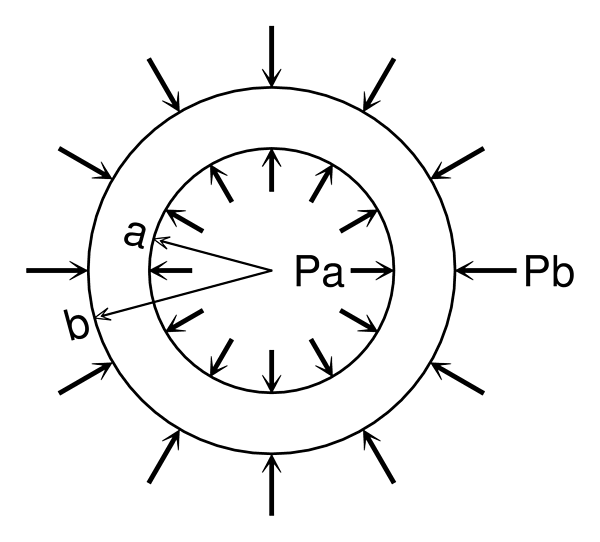
ここで一般論として極座標系において半径方向座標 $a$ に内圧 $P_a$ ,半径方向座標 $b$ に外圧 $P_b$ が作用する厚肉円筒を考えると,
この円筒内の任意の位置 $r$ における半径方向応力 $\sigma_r$ および円周方向応力 $\sigma_{\theta}$ は,引張を正として,
\begin{align}
&\sigma_r=\cfrac{a^2}{b^2-a^2}\left(1-\cfrac{b^2}{r^2}\right)\cdot P_a-\cfrac{b^2}{b^2-a^2}\left(1-\cfrac{a^2}{r^2}\right)\cdot P_b \tag{8}\\
&\sigma_{\theta}=\cfrac{a^2}{b^2-a^2}\left(1+\cfrac{b^2}{r^2}\right)\cdot P_a-\cfrac{b^2}{b^2-a^2}\left(1+\cfrac{a^2}{r^2}\right)\cdot P_b \tag{9}
\end{align}
ここで,水圧鉄管は無限地盤の中に埋設されているとすれば,岩盤の内縁部(コンクリート外縁部)および十分離れた岩盤の外縁部の条件は,以下の通り.
\begin{align}
& a=r_c & \qquad & b\rightarrow\infty \notag \\
& P_a=\frac{(P-P_s)r_s}{r_c} & \qquad & P_b=0 \notag
\end{align}
これらより,岩盤の半径方向および円周方向応力は以下の通りとなる.
\begin{align}
&\sigma_r=-\frac{(P-P_s)\cdot r_s\cdot r_c}{r^2} \qquad\text{(圧縮応力)} \tag{10}\\
&\sigma_{\theta}=\frac{(P-P_s)\cdot r_s\cdot r_c}{r^2} \qquad\text{(引張応力)} \tag{11}
\end{align}
また岩盤の半径方向ひずみは,圧縮を正として,
\begin{equation}
\varepsilon_g=\frac{(1+\nu_g)\sigma_r}{E_g}=(1+\nu_g)\frac{(P-P_s)r_s r_c}{E_g}\frac{1}{r^2}
\end{equation}
(注意)
上式は, $\sigma_r=-\sigma_{\theta}$ であるため,平面応力・平面ひずみのいずれの場合についても成立する.
\begin{align}
&\text{平面応力の場合} & \varepsilon_g&=\frac{\sigma_r-\nu_g\sigma_{\theta}}{E_g} &=\frac{(1+\nu_g)\sigma_r}{E_g} \notag \\
&\text{平面ひずみの場合} & \varepsilon_g&=\frac{(1-\nu_g^2)\sigma_r-\nu_g(1+\nu_g)\sigma_{\theta}}{E_g}&=\frac{(1+\nu_g)\sigma_r}{E_g} \notag
\end{align}
岩盤の変形量は,岩盤のひずみを岩盤厚で積分したものとなるため,
\begin{equation}
\delta_g=\int_{r_c}^{\infty}\varepsilon_g dr=(1+\nu_g)\frac{(P-P_s)r_s}{E_g} \tag{12}
\end{equation}
鉄管背面間隙量
コンクリートおよび岩盤の塑性変形量は,それぞれの弾性変形量に比例するものとし,比例定数を $\beta_c$, $\beta_g$ とすれば,
\begin{align}
\Delta_c&=\beta_c\frac{(P-P_s)r_s}{E_c}\ln\left(\frac{r_c}{r_s}\right) \notag \\
\Delta_g&=\beta_g(1+\nu_g)\frac{(P-P_s)r_s}{E_g}
\end{align}
鉄管の温度降下 $\Delta T$ による間隙量は,
\begin{equation}
\Delta_s=\alpha_s\cdot\Delta T\cdot r_s
\end{equation}
以上により鉄管背面間隙量は,コンクリートの硬化収縮量 $\Delta_{sd}$ を考慮して,
\begin{align}
\delta_0&=\Delta_c+\Delta_g+\Delta_s+\Delta_{sd} \notag \\
&=\beta_c\frac{(P-P_s)r_s}{E_c}\ln\left(\frac{r_c}{r_s}\right)
+\beta_g(1+\nu_g)\frac{(P-P_s)r_s}{E_g}+\alpha_s\cdot\Delta T\cdot r_s+\Delta_{sd} \tag{13}
\end{align}
岩盤負担率の算定
(1)式に,(5)(7)(12)(13)式を代入することにより,次の(14)式が得られる.
\begin{equation}
\frac{P_s\cdot r_s^2}{E_s\cdot t}
=(1+\beta_c)\frac{(P-P_s)r_s}{E_c}\ln\left(\frac{r_c}{r_s}\right)
+(1+\beta_g)(1+\nu_g)\frac{(P-P_s)r_s}{E_g}
+\alpha_s\cdot\Delta T\cdot r_s+\Delta_{sd} \tag{14}
\end{equation}
(14)式に対し,(3)式の関係から $P_s$ を消去し $\lambda$ を求めると,次の(15)式が得られる.
\begin{equation}
\lambda=\cfrac{1-\cfrac{E_s}{P}\cdot\alpha_s\cdot\left(\Delta T+\cfrac{\Delta_{sd}}{\alpha_s r_s}\right)\cdot\cfrac{t}{r_s}}
{1+(1+\beta_c)\cdot\cfrac{E_s}{E_c}\cdot\cfrac{t}{r_s}\cdot\ln\left(\cfrac{r_c}{r_s}\right)
+(1+\beta_g)\cdot\cfrac{E_s}{E_g}\cdot(1+\nu_g)\cdot\cfrac{t}{r_s}} \tag{15}
\end{equation}
また,(4)(6)(10)(11)式より,鉄管・コンクリートおよび岩盤の発生応力を求めることができる.
以下に,それぞれの発生応力を,(3)式の関係から $P_s$ を消去し $\lambda$ を用いて表現したものを再掲する.
応力の符号は引張を正で記載している.
\begin{align}
&\sigma_s=\frac{P\cdot r_s}{t}\cdot(1-\lambda) &\text{鉄管応力} \tag{16}\\
&\sigma_c=-\lambda\cdot P\cdot\frac{r_s}{r} &\text{コンクリート応力} \tag{17}\\
&\sigma_r=-\lambda\cdot P\cdot\frac{r_s\cdot r_c}{r^2} &\text{岩盤半径方向応力} \tag{18}\\
&\sigma_{\theta}=\lambda\cdot P\cdot\frac{r_s\cdot r_c}{r^2} &\text{岩盤円周方向応力} \tag{19}
\end{align}
鉄管内径を $D$ ,トンネル掘削径を $D_R$ ,ポアソン数 $m_g~(=1/\nu_g)$ として,(15)(16)式を書き直すことにより,次に示す水門鉄管技術基準と同形の設計式となる.(本設計式ではコンクリートの硬化収縮量 $\Delta_{sd}$ を考慮)
\begin{align}
&\sigma_s=\frac{PD}{2t}(1-\lambda) \tag{20}\\
&\lambda=\cfrac{1-\cfrac{E_s}{P}\cdot\alpha_s\cdot\left(\Delta T+\cfrac{2\Delta_{sd}}{\alpha_s D}\right)\cdot\cfrac{2t}{D}}{1+(1+\beta_c)\cdot\cfrac{E_s}{E_c}\cdot\cfrac{2t}{D}\cdot\ln\left(\cfrac{D_R}{D}\right)+(1+\beta_g)\cdot\cfrac{E_s}{E_g}\cdot\cfrac{1+m_g}{m_g}\cdot\cfrac{2t}{D}} \tag{21}
\end{align}
更に(20)(21)式より, $\lambda$ を消去し,鉄管応力を許容応力 $\sigma_{sa}$ とすることにより,所要板厚 $t$ を次式により直接求めることが出来る.
\begin{equation}
t=\cfrac{\cfrac{PD}{\sigma_{sa}}\left\{(1+\beta_c)\cdot\cfrac{E_s}{E_c}\cdot\cfrac{1}{D}\cdot\ln\left(\cfrac{D_R}{D}\right)+(1+\beta_g)\cdot\cfrac{E_s}{E_g}\cdot\cfrac{1+m_g}{m_g}\cdot\cfrac{1}{D}+\cfrac{E_s}{P}\cdot\alpha_s\cdot\left(\Delta T+\cfrac{2\Delta_{sd}}{\alpha_s D}\right)\cdot\cfrac{1}{D}\right\}-1}{(1+\beta_c)\cdot\cfrac{E_s}{E_c}\cdot\cfrac{2}{D}\cdot\ln\left(\cfrac{D_R}{D}\right)+(1+\beta_g)\cdot\cfrac{E_s}{E_g}\cdot\cfrac{1+m_g}{m_g}\cdot\cfrac{2}{D}} \tag{22}
\end{equation}
岩盤の境界が有限で自由変形面の場合
(10)(11)式は,岩盤の境界が無限遠である条件で導いたものであるが,ここでは,岩盤の境界が有限( $r=r_g$ )で自由変形面である場合を考える.(8)(9)式に対し,
\begin{align}
& a=r_c & \qquad & b=r_g \notag \\
& P_a=\frac{(P-P_s)r_s}{r_c} & \qquad & P_b=0 \notag
\end{align}
とすれば,岩盤の半径方向および円周方向応力は以下のとおりとなる.
\begin{align}
&\sigma_r=\frac{(P-P_s)r_s r_c}{r_g^2-r_c^2}\left(1-\frac{r_g^2}{r^2}\right) \notag \\
&\sigma_{\theta}=\frac{(P-P_s)r_s r_c}{r_g^2-r_c^2}\left(1+\frac{r_g^2}{r^2}\right) \notag
\end{align}
岩盤の半径方向ひずみは,平面応力状態・平面ひずみ状態の双方を考慮すべく,以下の通りおく.
\begin{equation}
\varepsilon_g=A\cdot\sigma_r-B\cdot\sigma_{\theta}=\frac{r_s r_c(P-P_s)}{r_g^2-r_c^2}\left\{(A-B)-(A+B)\frac{r_g^2}{r^2}\right\} \qquad \text{(引張:正)}
\end{equation}
\begin{equation}
\left\{\begin{array}{lllll}
平面応力 & \quad & A=\cfrac{1}{E_g} & \quad & B=\cfrac{\nu_g}{E_g} \\
平面ひずみ & \quad & A=\cfrac{1-\nu_g^2}{E_g} & \quad & B=\cfrac{\nu_g(1+\nu_g)}{E_g} \\
\end{array}\right. \notag
\end{equation}
岩盤の変形量は,岩盤のひずみを岩盤厚で積分したものとなるため,圧縮を正として
\begin{equation}
\delta_g=\int_{r_c}^{r_g}\varepsilon_g dr=\frac{r_s r_c(P-P_s)}{r_g+r_c}\left\{(A+B)\frac{r_g}{r_c}-(A-B)\right\}
\end{equation}
以降は(14)(15)式を導いたのと同様の手順により,岩盤の境界が有限で自由変形面の場合の岩盤負担率が次式のとおり定まる.
\begin{equation}
\lambda=\cfrac{1-\cfrac{E_s}{P}\cdot\alpha_s\cdot\left(\Delta T+\cfrac{\Delta_{sd}}{\alpha_s r_s}\right)\cdot\cfrac{t}{r_s}}
{1+(1+\beta_c)\cdot\cfrac{E_s}{E_c}\cdot\cfrac{t}{r_s}\cdot\ln\left(\cfrac{r_c}{r_s}\right)
+(1+\beta_g)\cdot\cfrac{E_s\cdot r_c}{r_g+r_c}\cdot\cfrac{t}{r_s}\cdot\left\{(A+B)\cfrac{r_g}{r_c}-(A-B)\right\}} \tag{23}
\end{equation}
\begin{equation}
\left\{\begin{array}{lllll}
平面応力 & \quad & A+B=\cfrac{1+\nu_g}{E_g} & \quad & A-B=\cfrac{1-\nu_g}{E_g} \\
平面ひずみ & \quad & A+B=\cfrac{1+\nu_g}{E_g} & \quad & A-B=\cfrac{(1+\nu_g)(1-2\nu_g)}{E_g} \\
\end{array}\right. \notag
\end{equation}
References
水門鉄管技術基準 水圧鉄管解説追補,pp109-114,(社)水門鉄管協会,1974.6.

